Bạn đã từng gặp khó khăn khi phải liệt kê tất cả các trường hợp trong các bài toán có số lượng lớn? Bạn đang tìm một phương pháp giải quyết đơn giản hơn cho những bài toán như vậy? Hãy cùng tìm hiểu về chỉnh hợp lặp và tổ hợp lặp, hai khái niệm quan trọng trong toán rời rạc, để giải quyết những bài toán phức tạp một cách dễ dàng hơn.
I. Chỉnh hợp lặp
Định nghĩa
Chỉnh hợp lặp chập k của n phần tử là một dãy gồm k phần tử từ tập A, trong đó mỗi phần tử có thể được lặp lại nhiều lần và có thứ tự nhất định.
Công thức chỉnh hợp lặp chập k của n phần tử
F(n^k) = n^k
II. Tổ hợp lặp toán rời rạc
Tổ hợp lặp là gì?
Tổ hợp lặp chập k của n phần tử là một dãy gồm k phần tử từ tập A, trong đó mỗi phần tử có thể được lặp lại nhiều lần (không tính đến thứ tự sắp xếp của chúng).
Công thức tổ hợp lặp
K(n^k) = C(n+k-1)^k = C(n+k-1)^(n-1)
III. Bài tập chỉnh hợp lặp có lời giải
Bài 1: Có bao nhiêu chuỗi có độ dài r có thể được hình thành từ chữ cái hoa trong bảng chữ cái tiếng Anh?
Lời giải: Mỗi chữ cái có 26 lựa chọn. Vì vậy, theo công thức chỉnh hợp lặp, có 26^r chuỗi có độ dài r.
IV. Bài tập tổ hợp lặp có lời giải
Bài 1: Có bao nhiêu cách để chọn 4 quả từ một đĩa chứa táo, cam, lê, nếu thứ tự các quả được chọn không quan trọng, chỉ quan trọng loại quả và số lượng quả, và có ít nhất bốn quả mỗi loại trong đĩa?
Lời giải: Cách để chọn 4 quả từ mỗi loại trái cây trong đĩa là số tổ hợp lặp chập 4 từ tập 3 phần tử {Táo, Cam, Lê}. Công thức để tính tổ hợp lặp là C(n+k-1)^k = C(3+4-1)^3-1 = 15.
4 Táo 4 Cam 4 Lê 3 táo, 1 cam 3 táo, 1 lê 2 táo, 2 cam 2 táo, 1 cam, 1 lê 3 cam, 1 lê 3 cam, 1 táo 2 cam, 2 lê 2 cam, 1 táo, 1 lê 3 lê, 1 táo 3 lê, 1 cam 2 lê, 2 táo 2 lê, 1 cam, 1 táo
Bài 2: Có bao nhiêu cách để chọn năm tờ tiền từ một hộp chứa các mệnh giá 1 đồng, 2 đồng, 5 đồng, 10 đồng, 20 đồng, 50 đồng, và 100 đồng? Giả sử rằng thứ tự các tờ tiền được chọn không quan trọng, và rằng các tờ tiền cùng mệnh giá là không phân biệt, và có ít nhất năm tờ tiền cho mỗi mệnh giá.
Lời giải: Số cách chọn 5 tờ tiền là C(n+k-1)^n-1 = C(5+7-1)^5-1 = 330.
Bài 3: Phương trình sau có bao nhiêu lời giải: x1 + x2 + x3 = 13, trong đó x1, x2, x3 là các số nguyên không âm?
Lời giải: Một lời giải tương ứng với một cách chọn 13 phần tử từ tập {a, b, c}, sao cho:
- có x1 lần lấy phần tử a,
- có x2 lần lấy phần tử b,
- có x3 lần lấy phần tử c.
Số lời giải là số tổ hợp lặp chập 13 từ một tập có 3 phần tử: C(n+k-1)^n-1 = C(3+11-1)^3-1 = 66 lời giải.
Bài 4: Phương trình sau có bao nhiêu lời giải: x1 + x2 + x3 + x4 = 20, trong đó x1, x2, x3 là các số nguyên thỏa (x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0)?
Lời giải:

Bài 5: Phương trình sau có bao nhiêu lời giải: x1 + x2 + x3 + x4 = 20, trong đó x1, x2, x3 là các số nguyên thỏa (x1 ≥ 6, x2 ≥ 3, x3 ≥ 9, x4 ≥ 2)?
Lời giải:
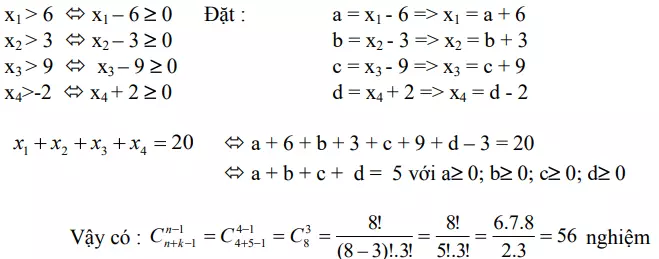
Bài 6: Bất phương trình sau có bao nhiêu lời giải: x1 + x2 + x3 ≤ 11, trong đó x1, x2, x3 là các số nguyên thỏa (x1 ≥ 0, x2 ≥ 0, x3 ≥ 0)?
Lời giải:
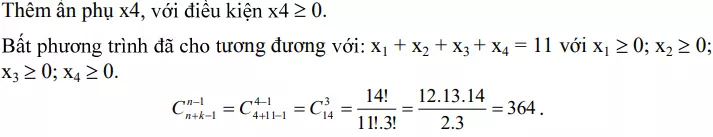
Bài 7: a) Giả sử chúng ta có 5 viên bi giống nhau và 3 chiếc túi khác màu là xanh, vàng và đỏ. Cho biết có bao nhiêu cách bỏ bi vào các túi?
Lời giải:
b) Giả sử chúng ta có 5 viên bi (2 bi sắt, 2 bi chai và 1 bi đất) và 3 chiếc túi màu xanh, vàng và đỏ. Cho biết có bao nhiêu cách bỏ bi vào các túi? Ví dụ: Cách 1 túi xanh chứa 2 bi sắt, túi vàng 2 bi chai và túi đỏ 1 bi đất; cách 2 -> túi xanh 1 bi sắt, túi vàng 2 bi chai + 1 bi sắt và túi đỏ 1 bi đất, ...
Lời giải:

Có rất nhiều bài toán thú vị liên quan đến chỉnh hợp lặp và tổ hợp lặp trong toán rời rạc. Hi vọng qua bài viết này bạn đã có cái nhìn tổng quan và một số lời giải cho những bài tập này. Hãy tiếp tục khám phá thêm các nguyên lý và ứng dụng khác của toán rời rạc trên ttnguyen.net để trở thành một nhà toán học thành công.












