Có một khái niệm quan trọng trong lĩnh vực điện tử gọi là Mạng Bốn Cực (MBC). Mạng Bốn Cực được định nghĩa là mạng có 4 thành phần, trong đó 1-1’ là đầu vào và 2-2’ là đầu ra. Lý thuyết MBC nghiên cứu về quan hệ giữa 4 đại lượng X, Y, Z, và A thông qua các thông số bên trong mạng. Để xây dựng lý thuyết này, cần thiết lập 6 hệ phương trình đặc trưng.
Hệ phương trình tham số Y
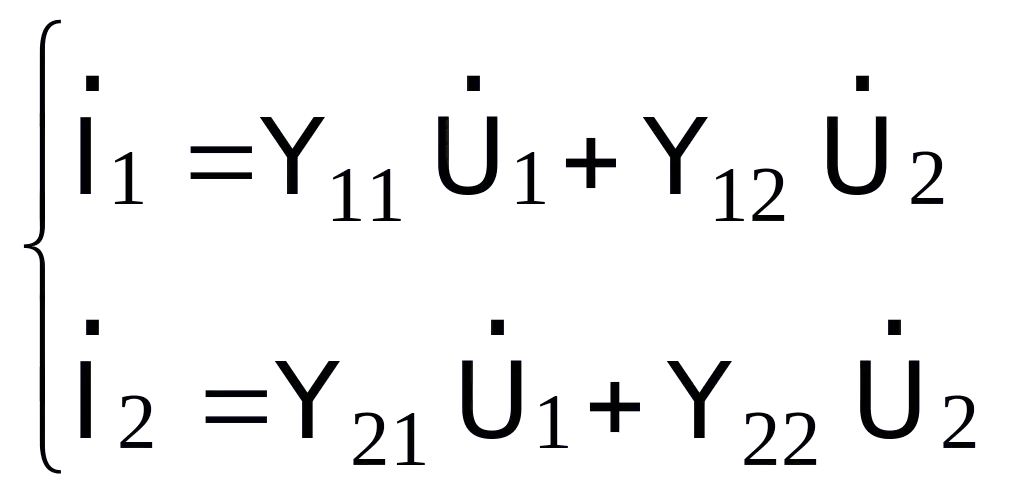(5.1)
Hệ phương trình tham số Z
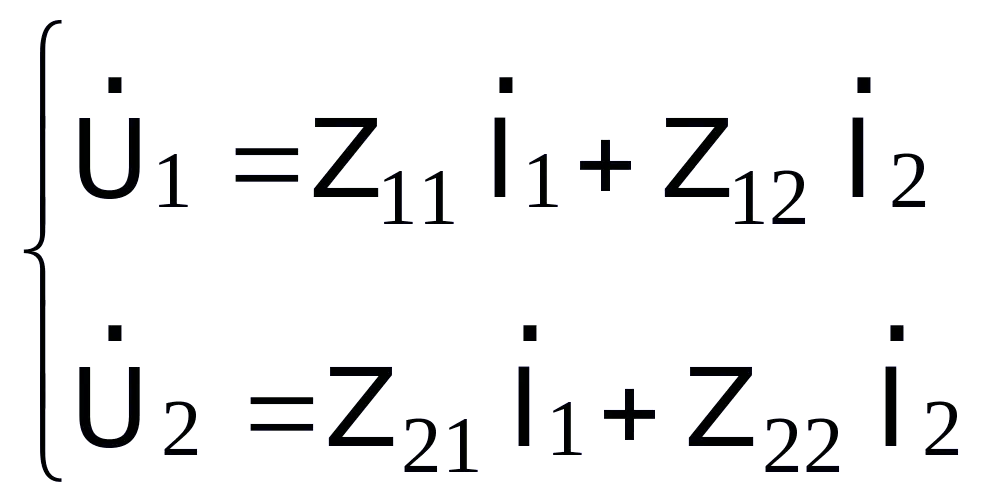(5.2)
Hệ phương trình tham số H
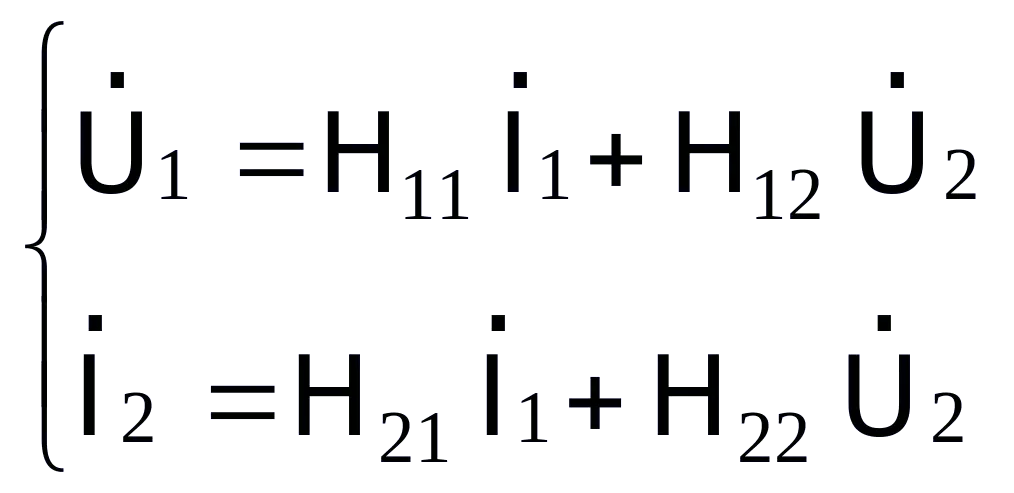(5.3)
Hệ phương trình tham số F
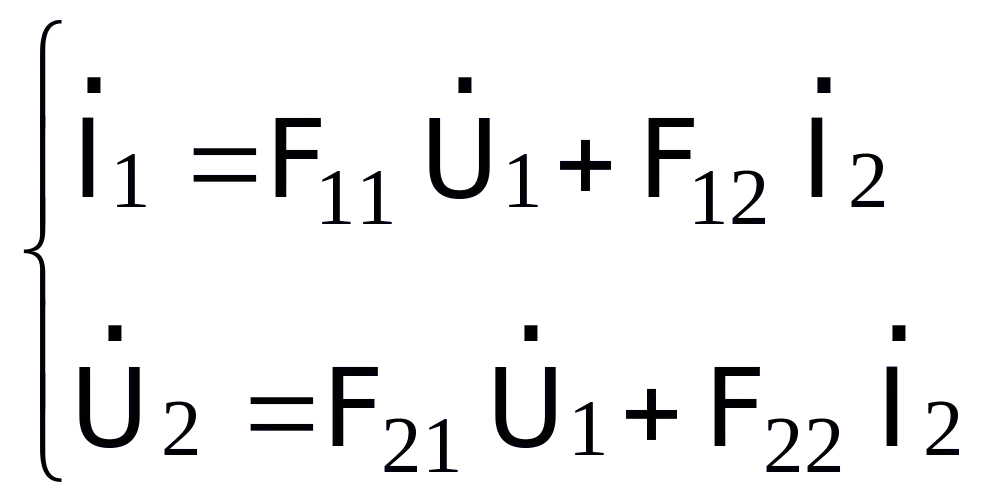(5.4)
Hệ phương trình tham số A
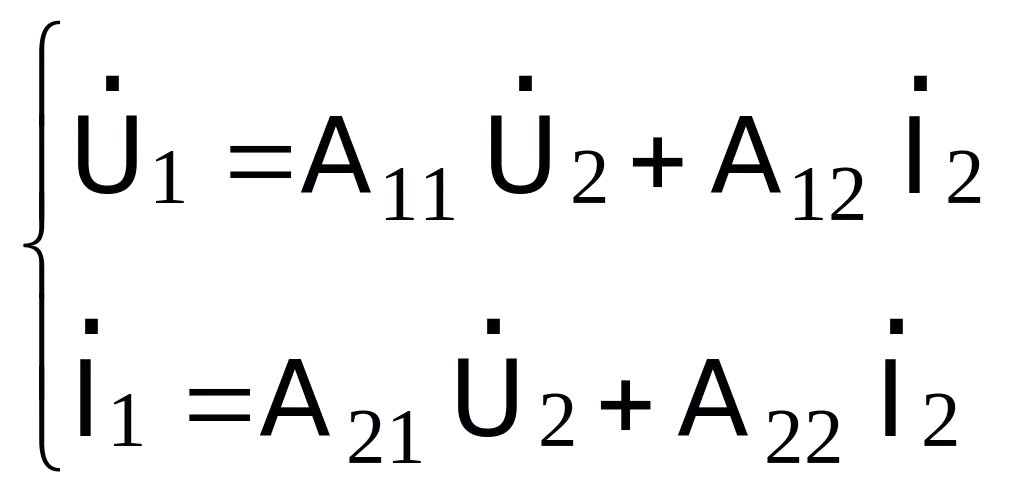(5.5)
Hệ phương trình tham số B
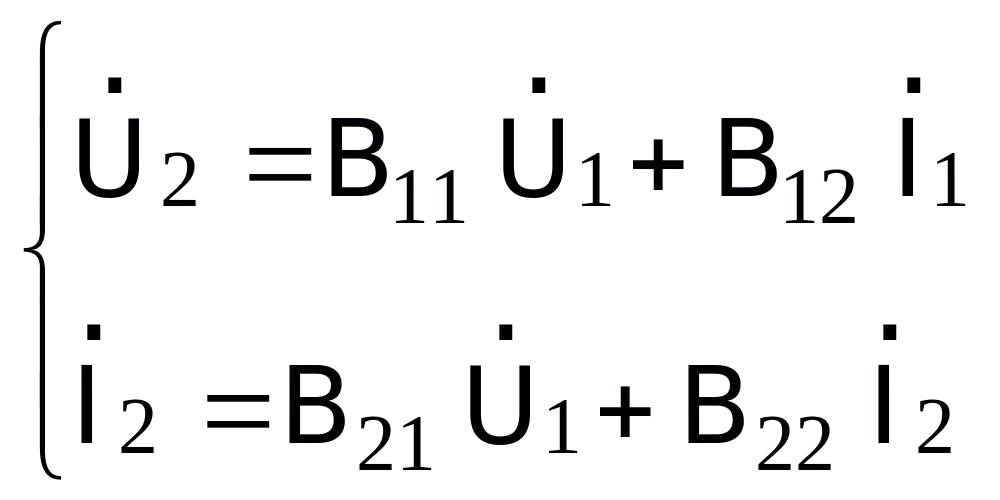(5.6)
Trong các hệ phương trình trên, hệ phương trình (5.5), (5.1), (5.2) và (5.3) được sử dụng nhiều nhất.
Liên hệ giữa các hệ tham số của MBC được mô tả bởi các phương trình sau:
-
Nếu MBC thuận nghịch, tức mạch tương hỗ (RLC thụ động) thì: Y12 = Y21; Z12 = Z21 (5.6)
-
Nếu MBC thuận nghịch đối xứng thì: Y12 = Y21; Z12 = Z21; Y11 = Y22; Z11 = Z22; A11 = A22 (5.7)
-
Nếu MBC thuận nghịch (RLC thụ động) thì: IAI = A11A22 - A12A21 = 1 (5.8)
Các hệ phương trình và quan hệ giữa các hệ tham số cung cấp cơ sở để nghiên cứu và tính toán các đặc tính của MBC.
Các MBC ghép
MBC thứ nhất có tham số [X'], MBC thứ hai có tham số [X'']. Khi ghép hai MBC này, ta được MBC ghép có tham số [X].
Hai MBC có thể được ghép liên thông, ghép song song hoặc ghép nối tiếp.
Hai MBC ghép liên thông: 
Hai MBC ghép song song: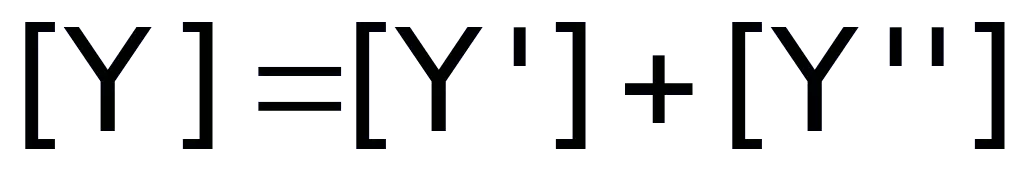 
Hai MBC ghép nối tiếp: [Z] = [Z'] + [Z'']
Hai MBC ghép nối tiếp đầu vào, song song đầu ra: [H] = [H'] + [H'']
Hai MBC ghép song song đầu vào, nối tiếp đầu ra: [F] = [F'] + [F'']
Tổng trở đầu vào của MBC
Khi mắc tải Z2 ở 2-2’ (hình 4.2a), ta có: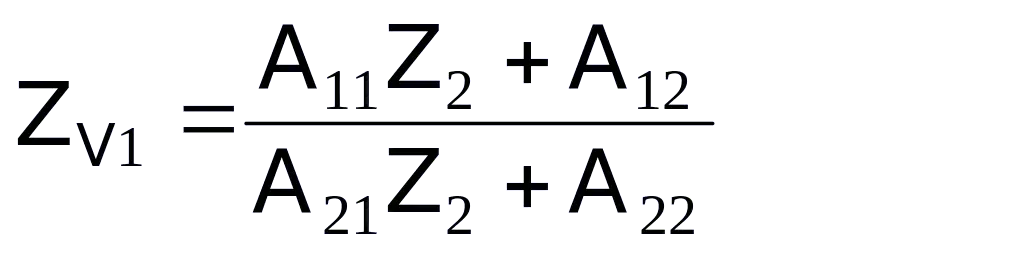 
(5.18)
Khi mắc tải Z1 ở 1-1’ (hình 5.2b), ta có: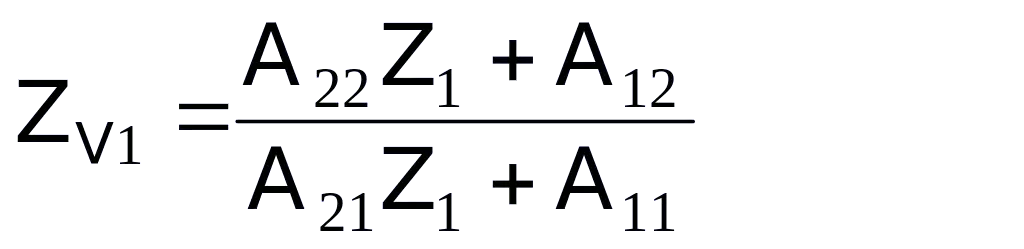 
(5.18)
Tổng trở đặc tính của MBC được tính bằng công thức: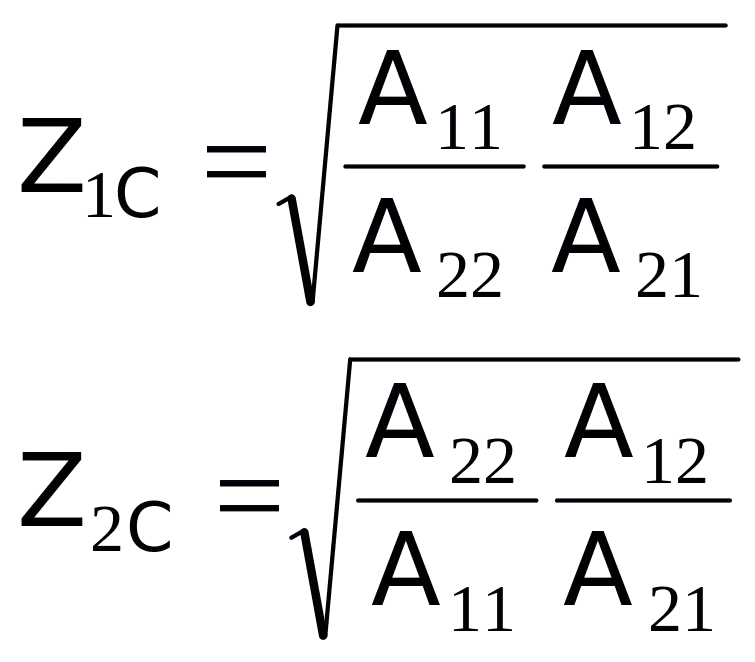 
(5.19)
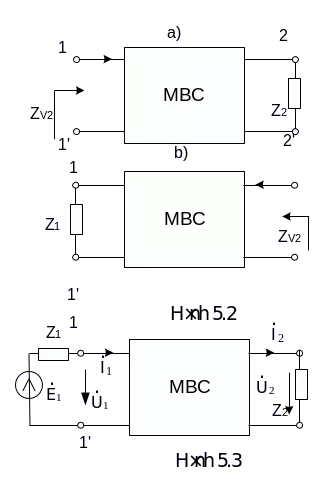
Nếu MBC đối xứng, tức Z1C = Z2C =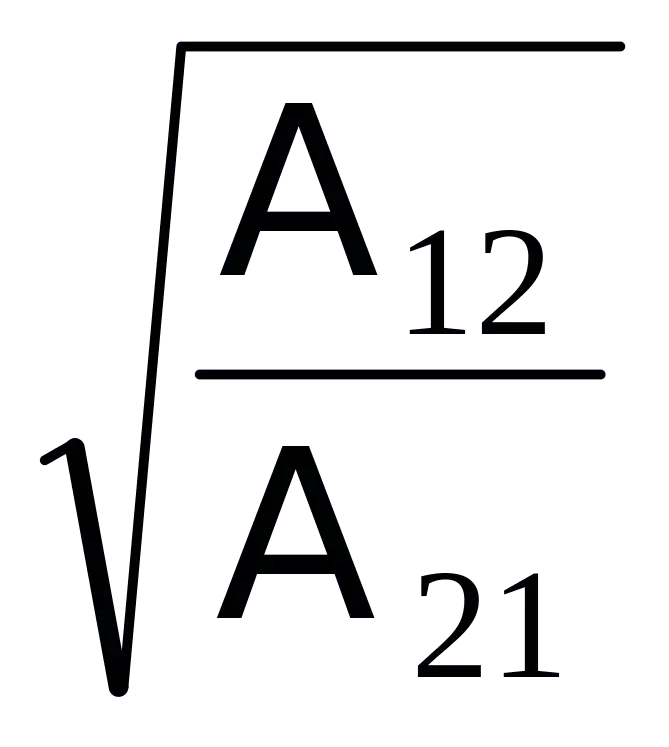 
Hàm truyền của MBC
Hàm truyền của MBC là một biểu thức phức gồm 4 thành phần: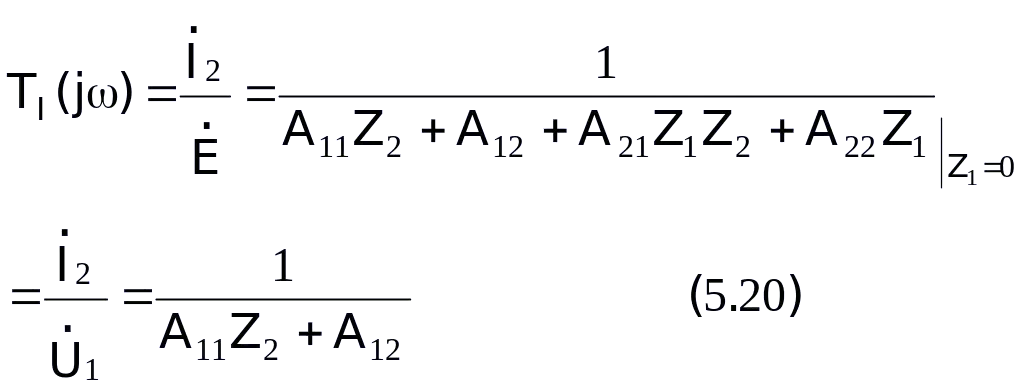 
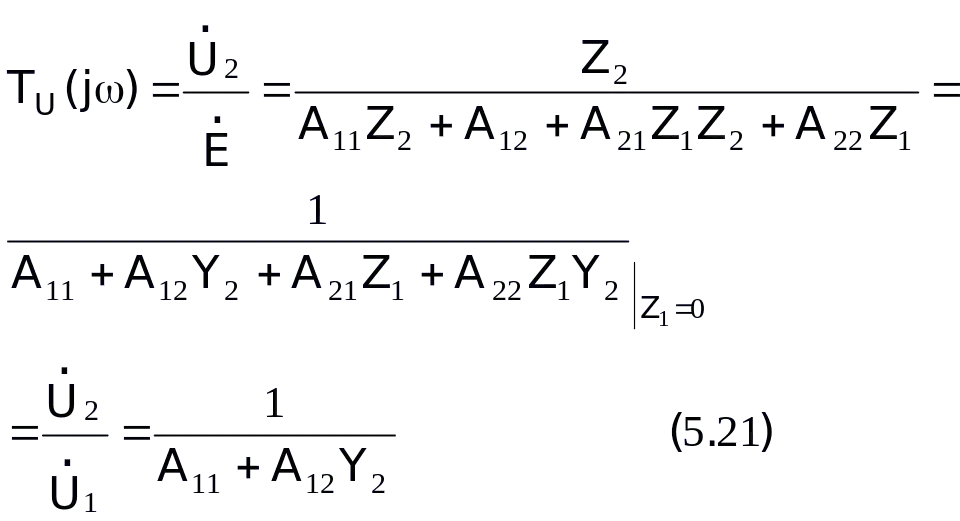
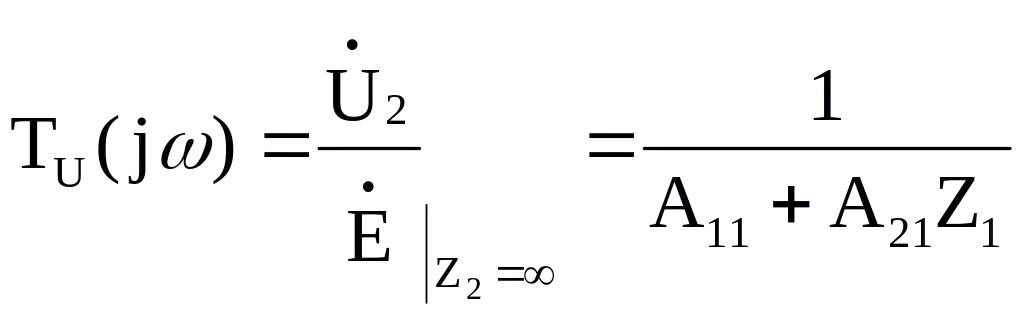(5.22)
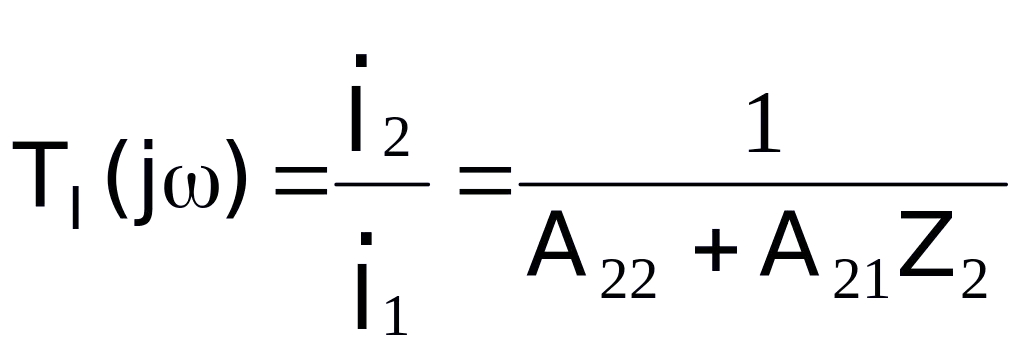(5.23)
Khi Z1 = R1 và Z2 = R2, ta có: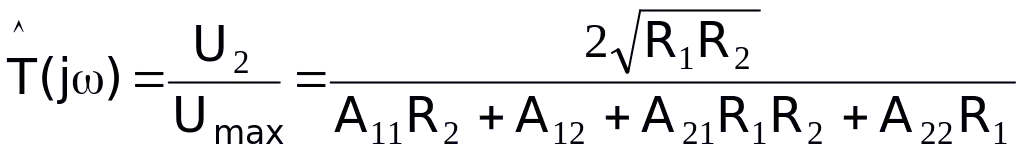 
(5.24)
Hằng số truyền đặc tính của MBC được tính bằng công thức: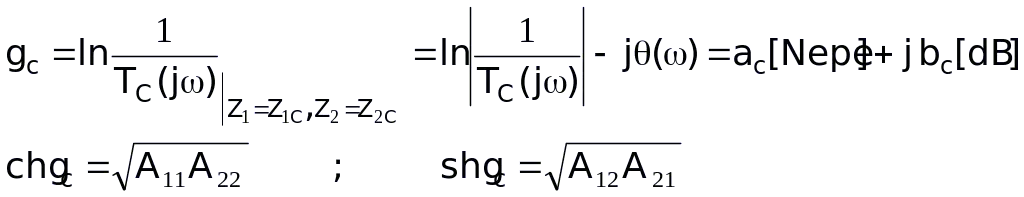 
(5.25)
Bài tập
5.1. Cho MBC hình Γ trên hình 5.4.
a) Hãy xác định hệ tham số A của MBC này bằng phương pháp ngắn và hở mạch 1-1’, 2-2’ theo hệ phương trình (5.5). b) Dùng công thức (5.9), (5.11) biến đổi về hệ tham số Y và Z. c) Kiểm chứng lại kết quả hệ tham số Y bằng phương pháp ngắn hở mạch 1-1’, 2-2’ theo hệ phương trình (5.1)
