Giai thừa là một phép tính toán trong toán học mà chắc chắn các bạn đã gặp trong các kỳ thi THPT Quốc gia. Trong bài viết này, chúng ta sẽ tìm hiểu lại công thức giai thừa và những bài tập vận dụng theo nhiều dạng thú vị.
Giai thừa là gì?
Giai thừa là phép tính toán trong toán học được sử dụng để tính tích của một dãy các số nguyên từ 1 đến một số nguyên dương nào đó. Ký hiệu của giai thừa là "!" (dấu chấm than). Giai thừa của một số nguyên dương n được ký hiệu là n! và được tính bằng cách nhân các số nguyên từ 1 đến n với nhau.

Ví dụ, giai thừa của số 5 được tính bằng: 5! = 5 x 4 x 3 x 2 x 1 = 120.
Giai thừa có nhiều ứng dụng trong toán học, đặc biệt là trong các vấn đề xác suất, tổ hợp và lý thuyết đồ thị. Nó cũng được sử dụng rộng rãi trong các lĩnh vực khác như khoa học máy tính, thống kê, vật lý và kỹ thuật.
Công thức giai thừa
Công thức tính giai thừa của một số nguyên dương n là:
n! = n × (n - 1) × (n - 2) × … × 2 × 1Với n! là ký hiệu giai thừa của số nguyên dương n.
Để minh họa, sau đây là một số ví dụ về tính giai thừa:
1! = 1
2! = 2 × 1 = 2
3! = 3 × 2 × 1 = 6
4! = 4 × 3 × 2 × 1 = 24
5! = 5 × 4 × 3 × 2 × 1 = 120Và cứ tiếp tục như vậy.
Cách tính giai thừa trên máy tính bỏ túi Casio fx 580VN Plus và fx 570VN Plus
Đa số các máy tính bỏ túi hiện nay có hỗ trợ tính giai thừa một cách nhanh chóng, các bạn chỉ cần nhập:
m → SHIFT → x- 1 → dấu "=".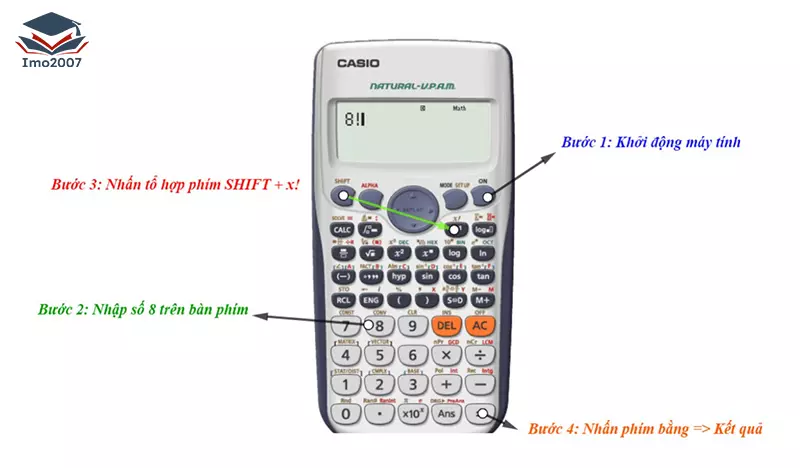
Ví dụ: Thực hiện tính các giai thừa sau bằng máy tính cầm tay: 5!, 9!.
Bấm 5!: 5 → SHIFT → x- 1 → dấu "=". Kết quả hiển thị trên máy tính: 5! = 120.
Bấm 9!: 9 → SHIFT → x- 1 → dấu "=". Kết quả hiển thị trên máy tính: 9! = 362880.
Những tính chất của giai thừa mà có thể bạn chưa biết
- Tính chất cơ bản: Giai thừa của số nguyên dương n được tính bằng cách nhân các số từ 1 đến n với nhau.
- Giai thừa của 0: Giai thừa của số 0 được định nghĩa là 1. Tức là 0! = 1.
- Quy tắc đệ quy: Giai thừa có thể được xác định theo quy tắc đệ quy như sau: n! = n × (n - 1)! Với điều kiện n > 0.
- Quy tắc đảo ngược: Giai thừa có tính chất đảo ngược, tức là n! = 1 / (n × (n - 1) × … × 2 × 1) = 1 / (n-1)!.
- Phép nhân giai thừa: Khi nhân một số nguyên dương n với giai thừa của một số nguyên dương m, ta có công thức: n × m! = (n × m)! / (m - 1)!.
- Quy tắc chia giai thừa: Khi chia giai thừa của một số nguyên dương n cho giai thừa của một số nguyên dương m (với n > m), ta có công thức: n! / m! = (n × (n - 1) × … × (m + 1)).
Một số bài toán vận dụng cách tính giai thừa
Sau khi đã hệ thống lại kiến thức về công thức giai thừa, hãy cùng giải một số dạng toán sau đây:
Bài tập 1: Tính giá trị của biểu thức (3! + 4!) / (2! + 5!)
Giải: Tính giai thừa của các số: 3! = 3 x 2 x 1 = 6, 4! = 4 x 3 x 2 x 1 = 24, 2! = 2 x 1 = 2, 5! = 5 x 4 x 3 x 2 x 1 = 120.
Tính giá trị của biểu thức: (3! + 4!) / (2! + 5!) = (6 + 24) / (2 + 120) = 30 / 122 ≈ 0.2459 (làm tròn 4 chữ số thập phân).
Vậy giá trị của biểu thức (3! + 4!) / (2! + 5!) là 0.2459.
Bài tập 2: Rút gọn biểu thức sau:
Giải: Dễ thấy, n - 1 lớn hơn n - 2 một đơn vị, do đó (n - 1)! = (n - 2)!(n - 1) và 6! = 4!5.6.
Bài tập 3: Giải phương trình sau:
Giải: Ta có điều kiện:
Ta sẽ tìm được x = 2, x = 3 (thỏa mãn điều kiện).
Như vậy, thông qua bài viết này các bạn đã hiểu thêm về công thức giai thừa cũng như các dạng bài tập thú vị. Để giỏi môn Toán, chúng ta cần nắm vững các công thức và các dạng toán khác nhau. Chúc các bạn luôn vững tâm chinh phục môn học này nhé.
Xem thêm: Bảng số nguyên tố dưới 10000 chuẩn và đầy đủ nhất.












