Lý thuyết nguyên hàm từng phần
Khái niệm nguyên hàm từng phần
Nguyên hàm từng phần là phương pháp giải các dạng bài toán 12 nguyên hàm. Khi cho hai hàm số u = u(x), v = v(x) có đạo hàm liên tục trên K, chúng ta có công thức nguyên hàm từng phần là ∫udv = uv−∫vdu.
Chú ý: Ta sử dụng phương pháp nguyên hàm từng phần nếu nguyên hàm có dạng I=∫f(x).g(x)dx, trong đó f(x) và g(x) là 2 trong 4 hàm số: Hàm số logarit, hàm số lượng giác, hàm số đa thức,...
Ví dụ về nguyên hàm từng phần
Ví dụ 1: Tìm nguyên hàm của hàm số sau: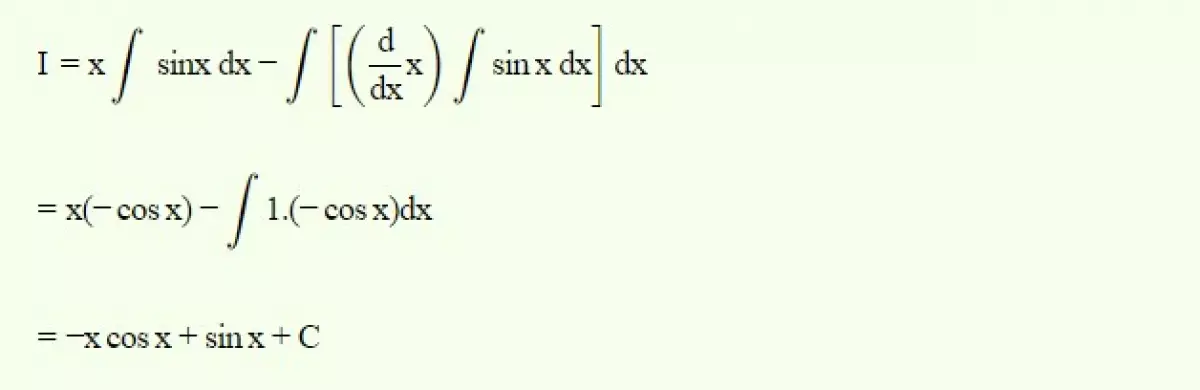 
Ta có: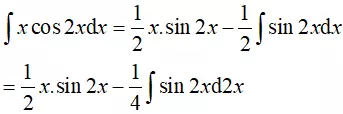 
Ví dụ 2: Hãy tìm nguyên hàm của hàm số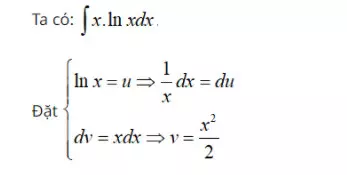 
? Giải: 
Ví dụ 3: Nguyên hàm của hàm số y=x.lnx là gì? Giải: 
Tổng hợp các công thức tính nguyên hàm từng phần
Cho 2 hàm số u = u (x) và v = v (x) có đạo hàm trên tập K. Khi đó ta có công thức tính nguyên hàm từng phần như sau:
Để tính nguyên hàm ∫f(x).g(x)dx, chúng ta làm theo công thức sau:
Bước 1: Ta đặt: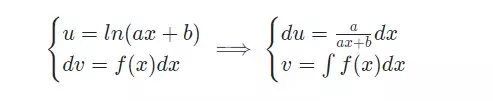 
Theo đó thì G(x) là một nguyên hàm bất kỳ của hàm số g(x).
- Bước 2.Lúc này theo công thức nguyên hàm từng phần ta có: 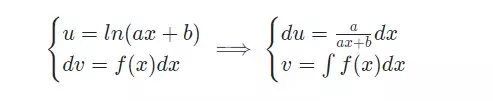= f(x).G(x)−∫G(x).f′(x)dx.
Lưu ý: Khi I=∫f(x).g(x)dx và f(x) và g(x) là 2 trong 4 hàm số: Hàm số logarit, hàm số đa thức, hàm số lượng giác, hàm số mũ ta đặt theo quy tắc đặt u.
Các em học sinh có thể nhớ cách đặt ẩn theo câu sau:
"Nhất log (bao gồm các hàm log, ln) - Nhì đa (tức là các hàm đa thức)
Tam lượng (tức là các hàm lượng giác) - Tứ mũ ( tức là các hàm mũ)"
Câu trên là thứ tự hàm số nào đứng trước trong câu, ta sẽ đặt u bằng hàm đó. Có nghĩa là:
-
Trong trường hợp nếu f(x) là hàm log, g(x) là một trong 3 hàm còn lại, ta sẽ đặt:
-
Tương tự, trong trường hợp nếu f(x) là hàm mũ, g(x) là hàm đa thức, ta sẽ đặt:
Xem thêm: Bảng công thức tính nguyên hàm đầy đủ nhất
Phương pháp giải nguyên hàm từng phần
Dạng 1: Tìm nguyên hàm của hàm số logarit
Hãy tính nguyên hàm của hàm số logarit sau: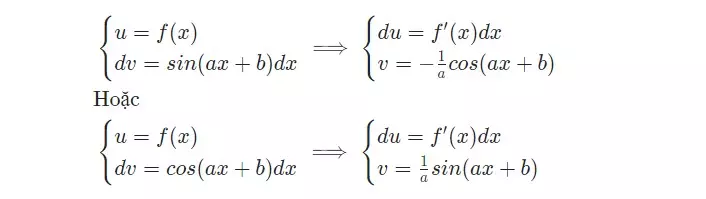 
với f(x) là một hàm của đa thức Phương pháp giải:
- Bước 1: Ta tiến hành đặt
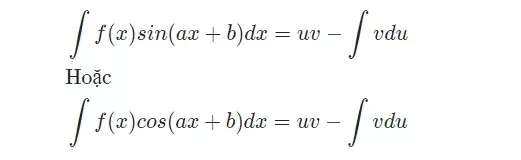
- Bước 2: Sau khi làm xong bước 1 ta biến đổi hàm số về dạng
Dạng 2: Nguyên hàm của hàm số mũ
Tính nguyên hàm của hàm số mũ sau: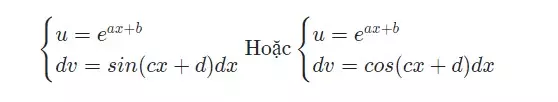 
với f(x) là một hàm đa thức Phương pháp:
- Bước 1: Ta tiến hành đặt
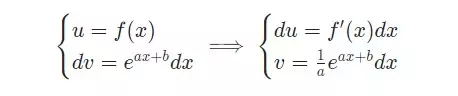
- Bước 2: Dựa vào bước đặt ở bước 1, ta có: ∫f(x).eax+b dx=uv-∫vdu
Dạng 3: Hàm số lượng giác và hàm đa thức
Hãy tính nguyên hàm của hàm số lượng giác: hoặc
Lời giải
-
Bước 1: Ta tiến hành đặt như sau:
-
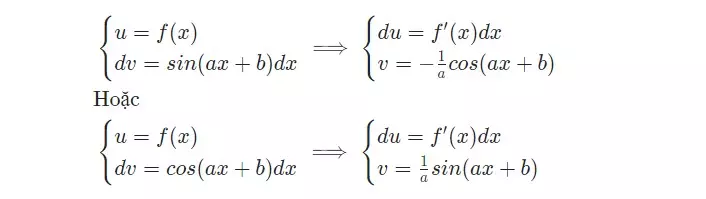
Bước 2: Ta biến đổi thành
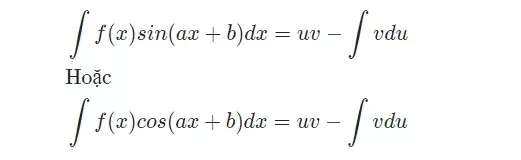
Dạng 4: Hàm số lượng giác và hàm số mũ
Hãy tính nguyên hàm kết hợp giữa hàm số lượng giác và hàm số mũ: hoặc
Các bước giải như sau:
- Bước 1: Ta tiến hành đặt như sau
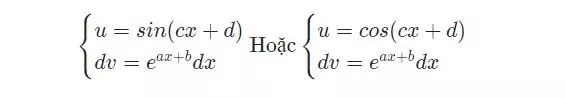
- Bước 2: Khi đó, nguyên hàm sẽ tính theo công thức tổng quát uv-∫vdu Lưu ý: Đây là dạng toán phức tạp nên cần lấy nguyên hàm từng phần 2 lần. Ngoài ra, ở bước 1 ta có thể đặt khác chút bằng cách đặt:
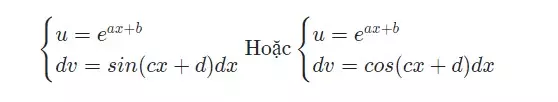
Cách giải dạng bài tập nguyên hàm từng phần có đáp án
Dạng 1: Tìm nguyên hàm của hàm số logarit
Ví dụ: Tìm nguyên hàm của hàm số f(x) = x.lnx Lời giải: Dựa vào phương pháp giải ở trên bạn dễ thấy
Bước 1: Ta tiến hành đặt biểu thức dạng
Bước 2: Theo công thức tính nguyên hàm từng phần, ta có:
Ví dụ: Hãy tính nguyên hàm của biểu thức sau I=∫xexdx Lời giải Dựa theo phương pháp trên, ta tiến hành đặt
Theo công thức tính nguyên hàm từng phần ta có:
Dạng 2: Hàm số lượng giác và hàm đa thức
Hãy tính nguyên hàm của hàm số lượng giác: hoặc
Lời giải
- Bước 1: Ta tiến hành đặt như sau:
- Bước 2: Dựa vào việc đặt ở bước 1, ta biến đổi thành
Dạng 4: Hàm số lượng giác và hàm số mũ Hãy tính nguyên hàm kết hợp giữa hàm số lượng giác và hàm số mũ: hoặc
Các bước giải như sau:
- Bước 1: Ta tiến hành đặt như sau
- Bước 2: Khi đó, nguyên hàm sẽ tính theo công thức tổng quát uv-∫vdu Lưu ý: Đây là dạng toán phức tạp nên cần lấy nguyên hàm từng phần 2 lần. Ngoài ra, ở bước 1 ta có thể đặt khác chút bằng cách đặt:
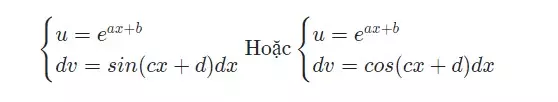
Dạng 1: Tìm nguyên hàm của hàm số logarit Ví dụ: Tìm nguyên hàm của hàm số f(x) = x.lnx Lời giải: Dựa vào phương pháp giải ở trên bạn dễ thấy Bước 1: Ta tiến hành đặt biểu thức dạng Theo công thức tính nguyên hàm từng phần, ta có:
