Trong lĩnh vực đại số và hình học giải tích, một trong những khái niệm quan trọng nhất là định thức ma trận. Nắm vững khái niệm này sẽ giúp chúng ta hiểu sâu hơn về cấu trúc và tính chất của ma trận, từ đó giải quyết các bài toán phức tạp. Hôm nay, mình xin giới thiệu với các bạn về cách tính định thức ma trận cấp 4.
1. Định thức ma trận là gì?
Định thức ma trận là một giá trị số được gán cho ma trận vuông. Det ma trận có thể được biểu diễn bằng hai dòng dọc hoặc chỉ đơn giản bằng cách ghi det và viết tên ma trận, ví dụ: |A|, det(A), det A.
=> Công thức tính giá trị định thức ma trận vuông cấp 2: |A| = (a{11} * a{22} - a{21} * a{12})
Ví dụ 1: Tính định thức bậc 2 sau:
| 1 2 | | 3 4 |=> Định thức ma trận bậc 2 = (1 4 - 3 2) = -2
2. Công thức tính định thức
- Công thức tính det cấp 2
- Công thức tính định thức cấp 3 (quy tắc Sarius):
|A| = (a_{11} * a_{22} * a_{33} + a_{21} * a_{32} * a_{13} + a_{12} * a_{23} * a_{31}) - (a_{13} * a_{22} * a_{31} + a_{11} * a_{23} * a_{32} + a_{12} * a_{21} * a_{33})Ví dụ 2: Giải định thức ma trận bằng phương pháp tam giác
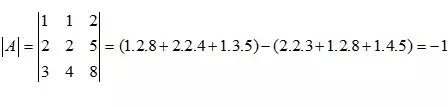Ví dụ 3: Tính định thức ma trận bằng phương pháp biến đổi siêu cấp
Một số tính chất cơ bản của định thức:
- Tính chất 1: det((A^{T})) = det(A)
- Tính chất 2: Đổi chỗ hai hàng (hoặc hai cột) của định thức cho nhau thì định thức đổi dấu.
- Tính chất 3: Khi nhân các phần tử của một hàng (hoạc một cột) với cùng một số k thì định thức được nhân lên k lần.
- Tính chất 4: Khi tất cả các phần tử của một hàng (hoặc một cột) có dạng tổng của hai số hạng thì định thức có thể phân tích thành tổng của hai định thức như sau:
3. Định thức con chính
Khái niệm: Định thức con là một ma trận con được tạo thành bằng cách chọn một số hàng và một số cột từ ma trận A ban đầu và xoá bỏ các hàng và cột còn lại.
Cho định thức của ma trận cấp 4 là:
| 1 2 3 4 | | 1 3 4 5 | | 3 4 5 6 | | 5 6 7 8 |Ta có:
- Định thức con chính cấp 1: | 1 |
- Định thức con chính cấp 2:
| 1 2 | | 1 3 |- Định thức con chính cấp 3:
| 1 2 3 | | 1 3 4 | | 3 4 5 |- Định thức con chính cấp 4: Ma trận ban đầu (định thức chính của ma trận cấp 4)
4. Tính định thức bằng phép biến đổi siêu cấp
Dưới đây là một số ví dụ về cách tính định thức bằng cách triển khai theo hàng:
Ví dụ 3: Tính định thức ma trận
Giải:
Các bước thực hiện:
- Nhân hàng 1 với -3 và cộng vào hàng 2 để xuất hiện phần tử 0
a21 = (-3) * 1 + 3 = 0 a22 = (-3) * 2 + 5 = -1 a23 = (-3) * (-1) + (-2) = 1 a24 = (-3) * 1 + 0 = -3-
Tương tự, nhân hàng 1 với -2 và cộng vào hàng 3, nhân hàng 1 với -2 và cộng vào hàng 1 để xuất hiện phần tử 0
-
Nhân hàng 2 với 2 và cộng vào hàng 3
-
Nhân hàng 3 với 1 và cộng vào hàng 4
Kết quả, định thức A chính là tích đường chéo: 1 (-1) 3 * 0 = 0
Bài 4: Giải định thức cấp 4 sau:
| 1 2 3 4 | | 1 3 4 5 | | 3 4 5 6 | | 5 6 7 8 |Giải:
Các bước thực hiện:
- Nhân hàng 1 với -5 và cộng vào hàng 4 để xuất hiện phần tử 0
a41 = (-5) * 1 + 5 = 0 a42 = (-5) * 2 + 6 = -4 a43 = (-5) * 3 + 7 = -8 a44 = (-5) * 4 + 8 = -12-
Tương tự, nhân hàng 1 với -3 và cộng vào hàng 3, nhân hàng 1 với -2 và cộng vào hàng 2, nhân hàng 1 với -1 và cộng vào hàng 1 để xuất hiện phần tử 0
-
Nhân hàng 2 với -1 và cộng vào hàng 3
-
Nhân hàng 3 với 1 và cộng vào hàng 4
Kết quả, định thức A chính là tích đường chéo: 1 (-4) 5 * (-12) = 240
5. Tính định thức ma trận 4×4
Để tìm định thức của một ma trận 4×4, chúng ta sử dụng phương pháp đơn giản, tương tự như khi tính định thức của một ma trận 3×3.
Trước khi tính định thức ma trận 4×4, chúng ta cần kiểm tra một số điều kiện trước:
- Kiểm tra xem có trường hợp nào mà định thức có thể bằng 0 không (ví dụ: toàn bộ hàng hoặc cột là 0).
- Kiểm tra xem có thể thực hiện việc phân tích một hàng hoặc cột không.
- Kiểm tra xem các phần tử của ma trận có giống nhau nhưng được sắp xếp lại trên bất kỳ cột hoặc hàng nào không.
Nếu bất kỳ trong ba trường hợp trên được đáp ứng, ta sử dụng các phương pháp tương ứng để tính toán định thức 3×3.
Công thức tính định thức cấp 4:
| a b c d | | e f g h | | i j k l | | m n o p |det(A) = aei(pl - on) - bfg(pk - ml) + cdg(nk - oj) - dhj(mg - ih)
Bài tập tính định thức cấp 4 có lời giải:
Bài 1: Giải định thức cấp 4 sau:
| 1 2 3 4 | | 1 3 4 5 | | 3 4 5 6 | | 5 6 7 8 |Giải:
Định thức ma trận 4×4 = 1 (3 5 8 + 4 6 5 + 5 4 6 - 7 5 6 - 5 4 8 - 3 6 * 8) = 240
Bài 2: Tính định thức ma trận cấp 4 có ẩn
| a b c d | | 1 2 3 4 | | e f g h | | i j k l |Giải:
Định thức ma trận 4×4 = a (2 g l + 3 k h + 4 f i - 3 g i - 2 f l - k h ) - b (1 g l + 3 c h + 4 i - d k - 3 g i - 4 c l) + c (...) - d * (...) = ...
Bài 3: Tính định thức cấp 4 sau:
| a 1 4 6 | | b 2 5 7 | | c 3 6 8 | | d 4 7 9 |Giải:
Định thức ma trận 4×4 = a (2 6 9 + 5 4 4 + 7 3 7 - 7 6 7 - 5 6 9 - 2 3 4) - 1 (b (6 9 + 5 4 3 + 7 6 4 - 7 6 3 - 5 6 9 - 2 4 7) - 1 (...) + 4 (...) - 6 * (...))
...
6. Định thức ma trận cấp 5×5
6.1 Cách tính định thức ma trận cấp 5×5
Dưới đây chúng ta sẽ sử dụng phương pháp triệt tiêu Gauss để tính định thức ma trận cấp 5:
Bước 1: Áp dụng phép biến đổi hàng và cột để đưa ma trận về dạng tam giác trên. Quá trình này bao gồm việc sử dụng các phép biến đổi sau:
- Nhân một hàng (hoặc cột) với một hằng số khác 0 để tạo ra các phần tử 0 ở dưới đường chéo chính.
- Cộng một hàng (hoặc cột) với một đa lượng của hàng (hoặc cột) khác để tạo ra các phần tử 0 dưới đường chéo chính.
Bước 2: Sau khi đưa ma trận về dạng tam giác trên, tính tích các phần tử trên đường chéo chính của ma trận. Kết quả này sẽ là det cấp 5.
6.2 Công thức tính định thức cấp 5
| a b c d e | | 1 2 3 4 5 | | f g h i j | | k l m n o | | p q r s t |det(A) = a (2 h n t + 3 m o e + 4 l i s + 5 k g * r - ...)
6.3 Bài tập tính định thức cấp 5 có lời giải
Bài 1: Tính định thức cấp 5 sau:
| 1 2 3 4 5 | | a b c d e | | f g h i j | | k l m n o | | p q r s t |Giải:
Dùng công thức tính định thức cấp 5 và tính toán từng phần tử theo quy tắc triệt tiêu Gauss.
Bài 2: Tính định thức cấp 5×5 sau:
| a 1 4 6 8 | | b 2 5 7 9 | | c 3 6 8 1 | | d 4 7 9 2 | | e 5 8 1 3 |Giải:
Dùng công thức tính định thức cấp 5 và tính toán từng phần tử theo quy tắc triệt tiêu Gauss.
Bài 3: Tính det ma trận cấp 5 sau:
| 1 2 3 4 5 | | 2 3 4 5 6 | | 3 4 
