Nguyên tắc căn bản khi học Toán là nắm vững kiến thức và áp dụng thực tế. Trong bài viết này, chúng ta sẽ tìm hiểu về cực trị hàm trùng phương, một khái niệm quan trọng được sử dụng rộng rãi trong học Toán. Chúng ta cũng sẽ xem qua một số bài tập về cực trị hàm trùng phương để hiểu rõ hơn về cách áp dụng kiến thức này.
Hàm trùng phương là gì?
Hàm trùng phương là một dạng đặc biệt của hàm số bậc 4 và thường được quy về hàm số bậc 2 để giải phương trình. Để tìm cực trị của hàm trùng phương, ta thường quy về phương trình bậc 2 để giải và tìm các giá trị của x.
Hàm số trùng phương có dạng như sau: (với a ≠ 0)
Đồ thị của hàm số trùng phương có thể có các đặc điểm như hình bên dưới:
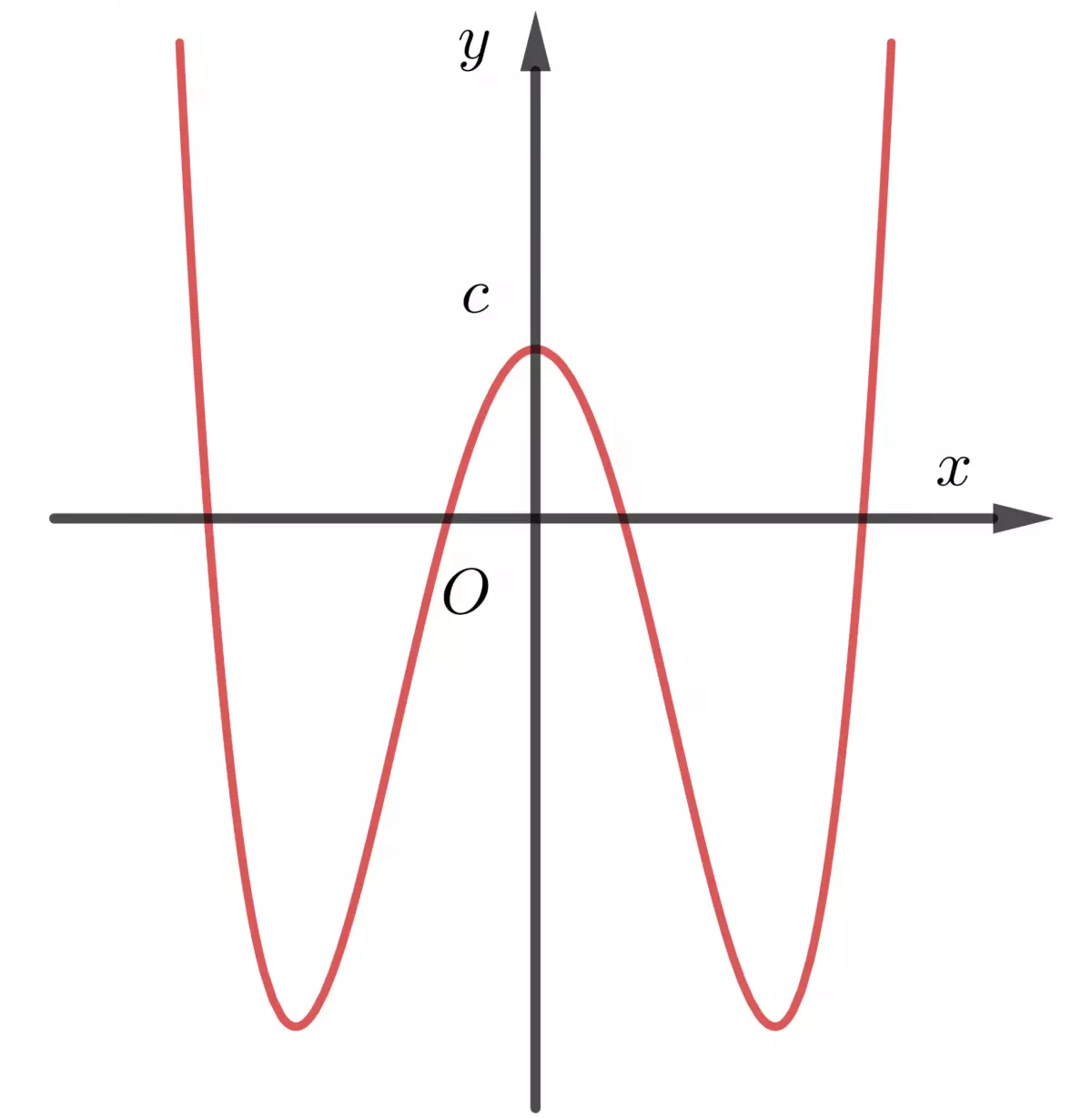
Điều kiện hàm trùng phương có 3 cực trị và 1 cực trị
Để hàm trùng phương có 3 cực trị và 1 cực trị, ta cần thỏa mãn các điều kiện sau:
Cho hàm số: (với a ≠ 0)
Khi đó, ta có:
- Khi a > 0, hàm số có 3 cực trị và 1 cực trị.
- Khi a < 0, hàm số không có cực trị và không có cực trị.
Công thức giải nhanh cực trị của hàm số trùng phương
Để giải nhanh và tìm các cực trị của hàm trùng phương, chúng ta cần nhớ một số tính chất quan trọng:
Tính chất 1: 3 điểm cực trị tạo thành một tam giác vuông cân
Cho hàm số có đồ thị (C).
Đồ thị (C) có 3 điểm cực trị nên y’=0 có 3 nghiệm phân biệt:
Khi , tam giác tạo thành là tam giác vuông cân. Công thức tính nhanh cho trường hợp này là:
Tính chất 2: 3 điểm cực trị tạo thành một tam giác đều
Cho hàm số:
Khi hàm số có 3 điểm cực trị, ta có công thức tính nhanh thỏa mãn:
Một số bài tập về cực trị hàm trùng phương
Để ôn tập kiến thức về cực trị hàm trùng phương, chúng ta hãy cùng làm một số bài tập dưới đây:
Bài 1: Tìm giá trị tham số m để hàm số có ba điểm cực trị tạo thành tam giác vuông cân
Cho hàm số:
Giải:
Ta có:
Hàm số có 3 cực trị .
Lúc này đồ thị có 3 điểm cực trị là:
A(0;m²)
B(-√(m+1);-2m-1)
C(√(m+1);-2m-1)
Có: B và C đối xứng qua trục Oy, A ∈ trục Oy nên tam giác ABC cân tại A.
Theo định lý Pitago ta có:
AB² + AC² = BC²
Bài 2: Xác định giá trị của m để hàm số có diện tích tam giác ABC bằng 64 và có 3 điểm cực trị
Cho hàm số:
Giải:
Ta có:
Hàm số có 3 điểm cực trị:
Bài 3: Tìm giá trị của m để hàm số có diện tích tam giác ABC bằng 64 và có 3 điểm cực trị
Cho hàm số:
Giải:
Ta có:
Hàm số có 3 điểm cực trị:
Bài 4: Tìm giá trị của m để hàm số có cực tiểu, cực đại và điểm cực trị của đồ thị hàm số tạo thành tam giác có góc bằng 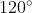
Cho hàm số:
Giải:
Ta có:
Đồ thị hàm số có các điểm cực trị là:
Góc chính là điểm A:
Bài 5: Tìm giá trị của m để hàm số có 3 điểm cực trị và ba điểm cực trị đó lập thành một tam giác có một góc bằng 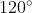
Cho hàm số:
Giải:
Ta có:
Hàm số có 3 điểm cực trị:
Vậy là giá trị cần tìm.
Sau bài viết này, hy vọng bạn đã hiểu rõ hơn về cực trị hàm trùng phương và cách áp dụng kiến thức này vào các bài tập. Đừng quên truy cập nền tảng học online Vuihoc.vn để có thêm nhiều tài liệu và bài giảng hữu ích nhé!












