Khái niệm về mặt phẳng
Trong cuộc sống hàng ngày, chúng ta thường thấy những mặt phẳng xung quanh chúng ta như trang giấy, mặt bảng, mặt nước trong hồ, mặt đường, và nhiều hơn nữa. Mặt phẳng không có giới hạn và không có độ dày, nó chỉ là một không gian phẳng.
Một điểm A thuộc mặt phẳng P được kí hiệu là A ∈ (P), tức là mặt phẳng P chứa điểm A. Ngược lại, một điểm B không thuộc mặt phẳng P được kí hiệu là B ∉ (P), tức là mặt phẳng P không chứa điểm B.
Hình biểu diễn của một hình không gian
Trong hình không gian, chúng ta sử dụng các hình biểu diễn để hiển thị các đối tượng. Có nhiều cách để biểu diễn một hình không gian.
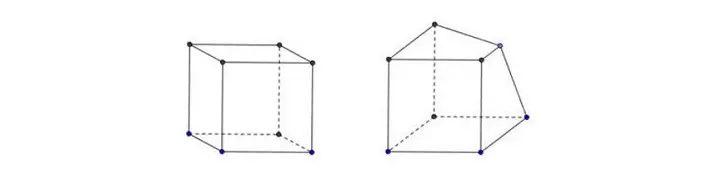Các quy tắc vẽ hình không gian bao gồm:
- Hình biểu diễn của đoạn thẳng là đoạn thẳng, của đường thẳng là đường thẳng.
- Hình biểu diễn của hai đường thẳng cắt nhau (hoặc song song) được biểu diễn thông qua hai đường thẳng cắt nhau (hoặc song song).
- Hình biểu diễn phải giữ nguyên mối quan hệ giữa đường thẳng và điểm.
- Sử dụng nét liền "_" để biểu diễn các đường nhìn thấy, và sử dụng nét đứt "-" để biểu diễn các đường bị khuất mà mắt không nhìn thấy được.
Một số tính chất thừa nhận
Tính chất số 1
Qua 2 điểm phân biệt không trùng nhau, chỉ có một và chỉ một đường thẳng đi qua 2 điểm đó.
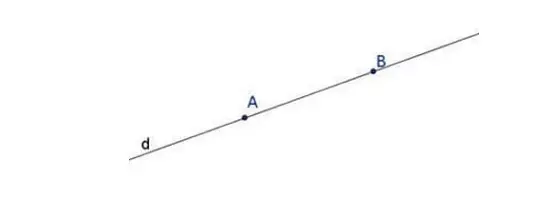
Tính chất số 2
Có một và chỉ một mặt phẳng đi qua 3 điểm phân biệt không thẳng hàng.
Tính chất số 3
Nếu trên một đường thẳng có 2 điểm chung phân biệt với một mặt phẳng thì mọi điểm của đường thẳng đều thuộc mặt phẳng đó.
Tính chất số 4
Tồn tại 4 điểm phân biệt không cùng một mặt phẳng.
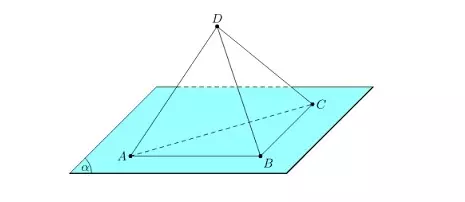
Tính chất số 5
Nếu hai mặt phẳng phân biệt có một điểm chung, thì 2 mặt phẳng đó sẽ có một đường thẳng chung duy nhất chứa tất cả các điểm chung của chúng.
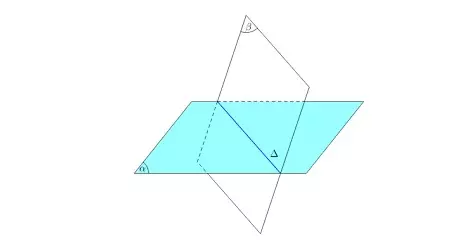
Tính chất số 6
Trên một mặt phẳng, mọi kết quả trong hình học phẳng đều đúng.
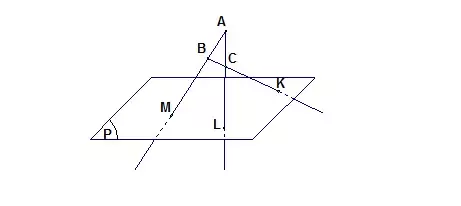
Cách xác định một mặt phẳng
Có 3 cách để xác định một mặt phẳng:
-
Chỉ cần ba điểm không thẳng hàng, sẽ có mặt phẳng duy nhất đi qua ba điểm đó. Mặt phẳng đó được kí hiệu là mp(ABC) hoặc (ABC).
-
Một mặt phẳng duy nhất đi qua một đường thẳng và một điểm không thuộc đường thẳng đó. Mặt phẳng đi qua điểm A và đường thẳng d không chứa điểm A được kí hiệu là mp(A;d) hoặc (A; d).
-
Một mặt phẳng duy nhất đi qua hai đường thẳng cắt nhau. Mặt phẳng qua hai đường thẳng a và b được kí hiệu là mp(a;b).
Hình chóp và hình tứ diện
Khái niệm hình chóp
Hình chóp là một hình học không gian được cấu tạo từ một đa giác được gọi là mặt đáy, và các tam giác có chung đỉnh được gọi là mặt bên. Đỉnh của hình chóp là điểm chung của các mặt bên.
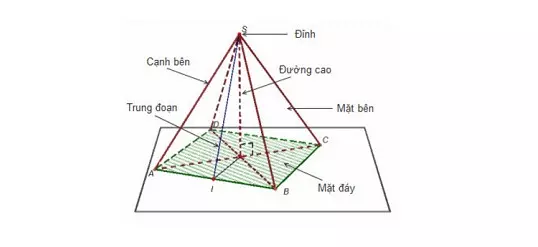
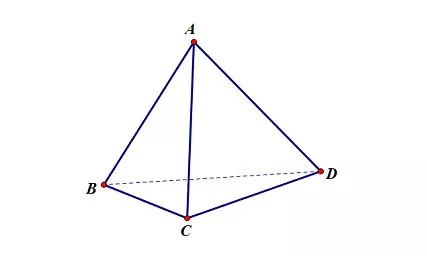
Khái niệm hình tứ diện
Hình tứ diện được tạo thành từ 4 điểm không đồng phẳng, và các mặt đều là tam giác.
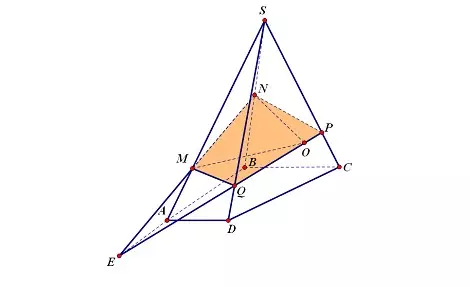
Thiết diện của hình chóp
Thiết diện cả hình chóp là một hình đa giác được tạo bởi mặt phẳng cắt qua hình chóp, với mỗi cạnh là giao tuyến của mặt phẳng đó với một mặt của hình tứ giác.
Ví dụ: Thiết diện MQPN của hình chóp với các cạnh được tạo bởi giao tuyến của (MQPN) giao với các mặt bên.
Các dạng bài tập cơ bản
Dạng bài tập 1: Xác định giao tuyến của 2 mặt phẳng
Để tìm giao tuyến của 2 mặt phẳng, ta cần xác định 2 điểm chung của 2 mặt phẳng. Đường thẳng đi qua 2 điểm đó chính là giao tuyến của 2 mặt phẳng.
Ví dụ: Cho hình chóp S.ABCD với đáy ABCD là một tứ giác. Ta có điểm M thuộc cạnh SA. Hãy tìm giao tuyến của các mặt phẳng sau: a. (SAC) và (SBD) b. (SAC) và (MBD) c. (MBC) và (SAD) d. (SAB) và (SCD)
Dạng bài tập 2: Chứng minh 3 điểm thẳng hàng chứng minh 3 đường thẳng đồng quy
Để chứng minh 3 điểm thẳng hàng, ta chứng minh các điểm này là điểm chung của 2 mặt phẳng phân biệt. Khi đó, chúng sẽ cùng nằm trên đường thẳng giao tuyến của 2 mặt phẳng, vì vậy chúng thẳng hàng.
Ví dụ: Cho tứ diện S.ABC. Trên các đoạn thẳng SA, SB và SC lấy các điểm D, E và F sao cho đoạn thẳng DE cắt đoạn AB tại I, EF giao với đoạn BC tại điểm J, đoạn thẳng FD cắt CA tại K. Chứng minh rằng 3 điểm I, J và K thẳng hàng.
Dạng bài tập 3: Tìm giao điểm của đường thẳng và mặt phẳng
Để tìm giao điểm của đường thẳng và mặt phẳng, ta sử dụng định nghĩa, các tính chất hay các biểu thức tọa độ của phép tịnh tiến.
Trường hợp 1: Nếu trong mặt phẳng đã cho có sẵn đường thẳng cắt đường thẳng đã cho tại điểm M, thì điểm M cũng chính là giao điểm của đường thẳng và mặt phẳng.
Trường hợp 2: Nếu trong mặt phẳng đã cho chưa có sẵn đường thẳng cắt đường thẳng đã cho, ta cần chọn một mặt phẳng khác chứa đường thẳng đã cho để tìm giao tuyến. Sau đó, tìm giao điểm của đường thẳng và giao tuyến đó trong mặt phẳng đã cho.
Trên đây là những kiến thức cơ bản về mặt phẳng và đường thẳng trong chương trình Toán 11. Hy vọng với bài viết này, bạn đã nắm được kiến thức cũng như các phương pháp giải các dạng bài tập liên quan đến phần này. Chúc bạn đạt được điểm cao trong các kì thi sắp tới.
