Double-precision floating-point format (FP64 or float64) is a widely used format for representing floating-point numbers in computer memory. With its ability to represent a wide dynamic range of numeric values, it has become the preferred choice when single precision falls short in terms of range or precision.
In the IEEE 754-2008 standard, this 64-bit base-2 format is officially referred to as binary64, while it was called "double" in the IEEE 754-1985 standard. Additional floating-point formats, such as 32-bit single precision and base-10 representations, have also been specified by IEEE 754.
Double precision has its origins in Fortran, which was one of the first programming languages to provide floating-point data types. Prior to the adoption of the IEEE 754-1985 standard, the representation and properties of floating-point data types varied across different computer manufacturers, models, and programming languages.
Let's dive deeper into the details of double-precision floating-point format.
Floating-point formats IEEE 754
IEEE 754 defines a range of floating-point formats to cater to different needs. Here are some of the most common formats:
- 16-bit: Half (binary16)
- 32-bit: Single (binary32), decimal32
- 64-bit: Double (binary64), decimal64
- 128-bit: Quadruple (binary128), decimal128
- 256-bit: Octuple (binary256)
- Extended precision
Apart from these, there are other floating-point formats like Minifloat, bfloat16, TensorFloat-32, Microsoft Binary Format, IBM floating-point architecture, PMBus Linear-11, and G.711 8-bit floats. There are also alternatives like arbitrary precision.
IEEE 754 double-precision binary floating-point format: binary64
The double-precision binary floating-point format, commonly known as "double," is widely used on PCs due to its broader range of values compared to single precision.
In the binary64 format, a number is represented using the following components:
- Sign bit: 1 bit
- Exponent: 11 bits
- Significand precision: 53 bits (52 explicitly stored)
The sign bit determines the sign of the number, including zero. The exponent field is an 11-bit unsigned integer from 0 to 2047, with a bias of 1023. Exponents range from -1022 to +1023, with some reserved for special numbers.
The 53-bit significand precision allows for around 15 to 17 significant decimal digits of precision. If a decimal string with at most 15 significant digits is converted to the binary64 format and back to decimal, the result should match the original string. However, if a binary64 number is converted to a decimal string with at least 17 significant digits and back, the result must match the original number.
The real value assumed by a given 64-bit double-precision datum can be calculated using the formula: (-1)^sign (1 + sum[i=1 to 52] (b[52-i] 2^-i)) * 2^(e-1023)
Here's an example of the binary64 format in action: 
Caption: The layout of a 64-bit double-precision floating-point number.
Exponent encoding
The exponent of a double-precision binary floating-point number is encoded using an offset-binary representation. The bias for the exponent is 1023, with some special values having specific meanings.
For example, an exponent value of 0 is used to represent subnormal numbers and signed zero. An exponent value of 2047 is used to represent infinity and NaN (Not a Number). All bit patterns are valid encodings, but the interpretation depends on the processor.
Here are some examples of exponent encodings:
- 00000000001 = 1: 2^(1-1023) = 2^-1022 (smallest exponent for normal numbers)
- 01111111111 = 1023: 2^(1023-1023) = 2^0 (zero offset)
- 10000000101 = 1029: 2^(1029-1023) = 2^6
- 11111111110 = 2046: 2^(2046-1023) = 2^1023 (highest exponent)
Precision limitations on integer values
Double-precision floating-point format allows for the exact representation of integers within the range of -2^53 to 2^53. Integers outside this range are rounded to the nearest representable multiple of a power of 2.
For example, integers between 2^n and 2^n+1 are rounded to a multiple of 2^n-52. The spacing as a fraction of the numbers in the range from 2^n to 2^n+1 is 2^n-52.
Implementations
Double precision is implemented in various programming languages, each with its own approach. Here are some examples:
C and C++
C and C++ offer a variety of arithmetic types, and while double precision is not required by the standards (except for IEEE 754 arithmetic in C99's optional annex), it is commonly implemented as double. However, on systems with extended precision by default, some compilers may not adhere to the C standard or may suffer from double rounding issues.
Fortran
Fortran provides several integer and real types, and the 64-bit real64 type, accessible via the iso_fortran_env module, corresponds to double precision.
Common Lisp
Common Lisp offers different floating-point types, including SHORT-FLOAT, SINGLE-FLOAT, DOUBLE-FLOAT, and LONG-FLOAT. The DOUBLE-FLOAT type corresponds to double precision.
Execution speed with double-precision arithmetic
Performing calculations with double-precision floating-point variables is generally slower than those with single precision. This performance difference is particularly noticeable in parallel code running on GPUs, where double precision calculations can take up to 32 times longer than single precision calculations, depending on the hardware.
Mathematical functions such as sin, cos, atan2, log, exp, and sqrt also require more computations to provide accurate double-precision results, making them slower compared to single-precision calculations.
Conclusion
Double-precision floating-point format, or float64, is a crucial format for representing floating-point numbers with a wider range and higher precision. Understanding its specifications, limitations, and implementations is essential for developing efficient and accurate computational systems.
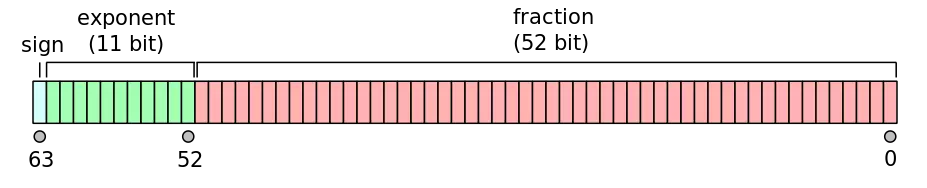Caption: Visualization of the double-precision binary floating-point format.
Remember, double precision is just one of the many floating-point formats available, each tailored to specific needs and requirements. By grasping the intricacies of double-precision floating-point format, you can make informed decisions when handling numeric data in your projects.
