Phương pháp thế là một trong những phương pháp giải hệ phương trình bậc nhất 2 ẩn được sử dụng rất phổ biến. Nhưng để thực hiện giải hệ phương trình bằng phương pháp thế, chúng ta cần nắm những kiến thức cơ bản và áp dụng chúng một cách chính xác. Hãy cùng HOCMAI tìm hiểu chi tiết về phương pháp này.
A. Các kiến thức cần nắm về giải hệ phương trình bằng phương pháp thế
Phương pháp thế là một trong những cách biến đổi tương đương trong giải hệ phương trình bậc nhất 2 ẩn. Để thực hiện phương pháp thế, chúng ta cần tuân thủ hai bước sau:
Bước 1: Từ một phương trình trong hệ phương trình đã cho, chúng ta biểu diễn một ẩn bất kỳ theo ẩn còn lại.
Bước 2: Thay thế phương trình đã biến đổi vào ẩn của phương trình còn lại, từ đó chúng ta sẽ thu được một phương trình chỉ có 1 ẩn duy nhất.
Bước 3: Giải phương trình mới 1 ẩn và sử dụng nghiệm đó thế vào 1 trong 2 phương trình của hệ để tìm kết quả của ẩn còn lại.
Lưu ý:
- Nếu hệ phương trình ra kết quả cả 2 ẩn đều bằng 0 thì hệ phương trình đó vô nghiệm.
- Phải giữ nguyên tập nghiệm của hệ phương trình đã cho khi tiềm nghiệm của phương trình 1 ẩn mới sau khi biến đổi.
B. Một số dạng bài thường gặp về giải hệ phương trình bằng phương pháp thế
Dạng 1: Giải hệ phương trình bằng phương pháp thế
Phương pháp giải:
Dựa vào phương pháp thế, chúng ta thực hiện các bước sau:
Bước 1: Rút x hoặc y từ một phương trình của hệ phương trình, thay vào phương trình còn lại, ta sẽ thu được phương trình mới chỉ còn một ẩn.
Bước 2: Giải phương trình 1 ẩn sau khi đã biến đổi ở bước 1, thay kết quả tìm được vào một trong 2 phương trình của đề bài để tìm kết quả còn lại.
Khi sử dụng phương pháp thế, ta nên chọn phương trình đơn giản nhất của hệ, thường là các phương trình có hệ số của một trong 2 ẩn đơn giản hoặc có hệ số nhỏ như 1 hoặc -1.
Dạng 2: Quy về hệ phương trình bậc nhất hai ẩn
Phương pháp làm bài: Để sử dụng phương pháp này, chúng ta thực hiện các bước sau:
Bước 1: Biến đổi hệ đã cho về dạng phương trình bậc nhất hai ẩn.
Bước 2: Áp dụng phương pháp giải của dạng 1 để giải phương trình mới đã biến đổi.
Dạng 3: Dạng sử dụng phương pháp đặt ẩn phụ
Bước 1: Phương pháp này được thực hiện khi có biểu thức chung trong các phương trình của hệ phương trình đã cho (ngoài ra chúng ta cũng có thể tự biến đổi để tạo ra biểu thức chung) để trở thành một hệ phương trình mới đơn giản, ngắn gọn hơn.
Bước 2: Áp dụng phương pháp như dạng 1 để tìm được kết quả của ẩn phụ rồi tìm nghiệm của hệ phương trình ban đầu.
Dạng 4: Tìm điều kiện của tham số để hệ phương trình thỏa mãn điều kiện cho trước.
Phương pháp:
Để giải được dạng bài này, chúng ta cần ghi nhớ tính chất sau:
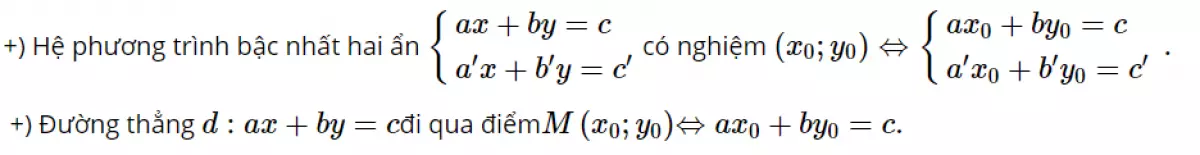
C. Các bài tập luyện tập




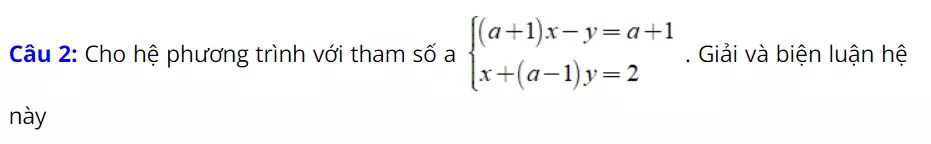

Giải bài tập sách giáo khoa giải hệ phương trình bằng phương pháp thế
Bài 12 (trang 15 SGK Toán 9 Tập 2): Sử dụng phương pháp thế giải các hệ phương trình sau
Hướng dẫn giải:


Bài 13 (trang 15 SGK Toán 9 Tập 2): Sử dụng phương pháp thế giải các hệ phương trình sau

Hướng dẫn giải:
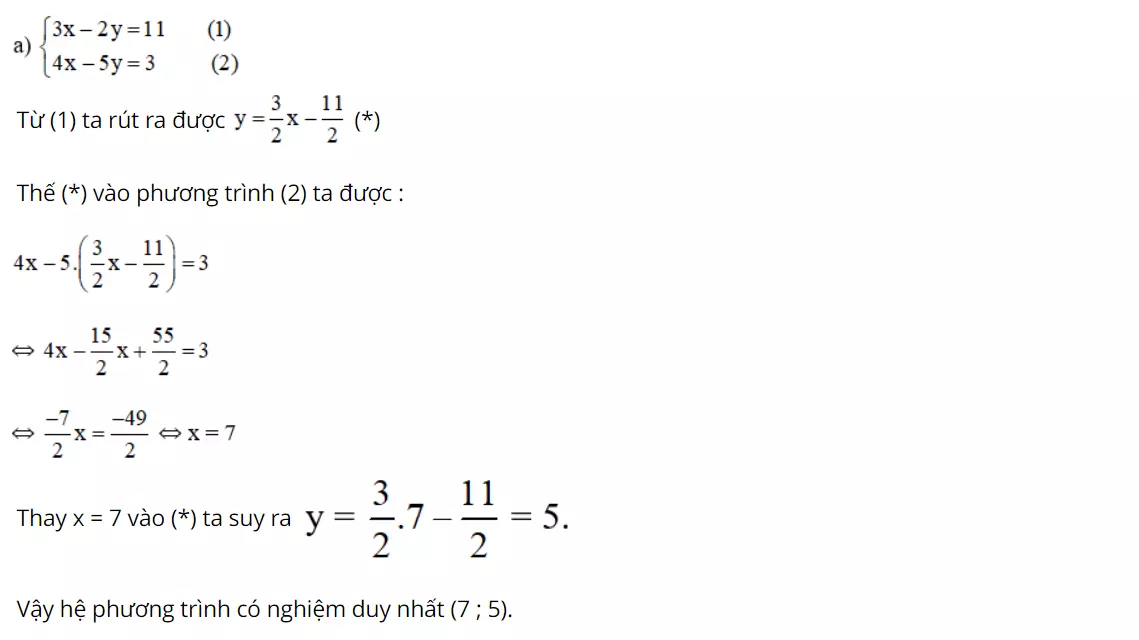
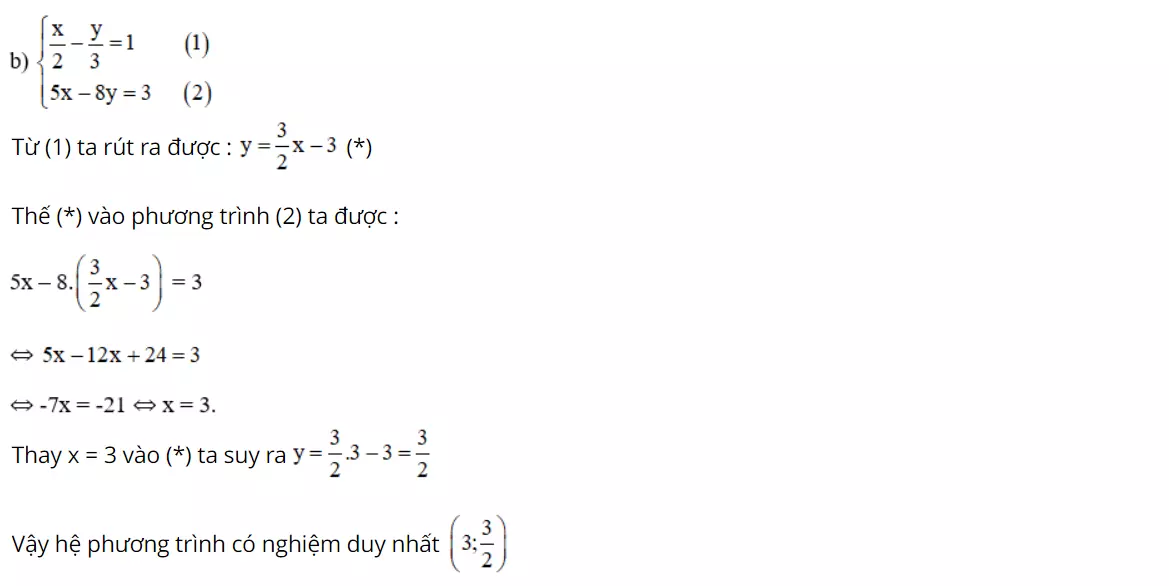
Bài 14 (trang 15 SGK Toán 9 Tập 2): Sử dụng phương pháp thế giải các hệ phương trình sau

Hướng dẫn giải:
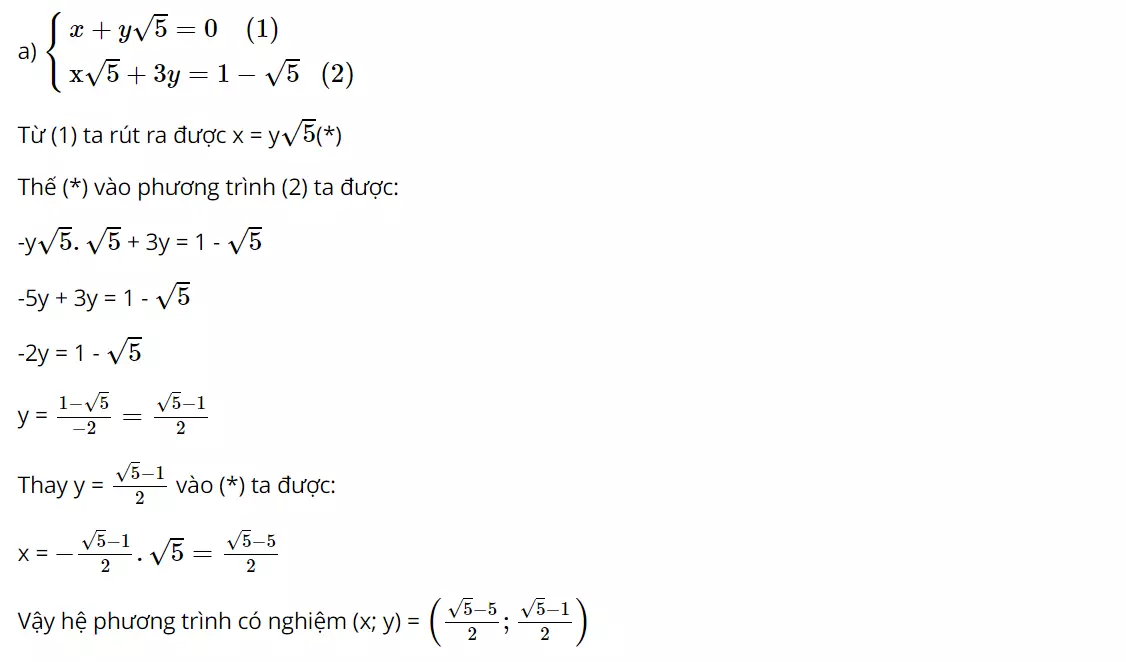
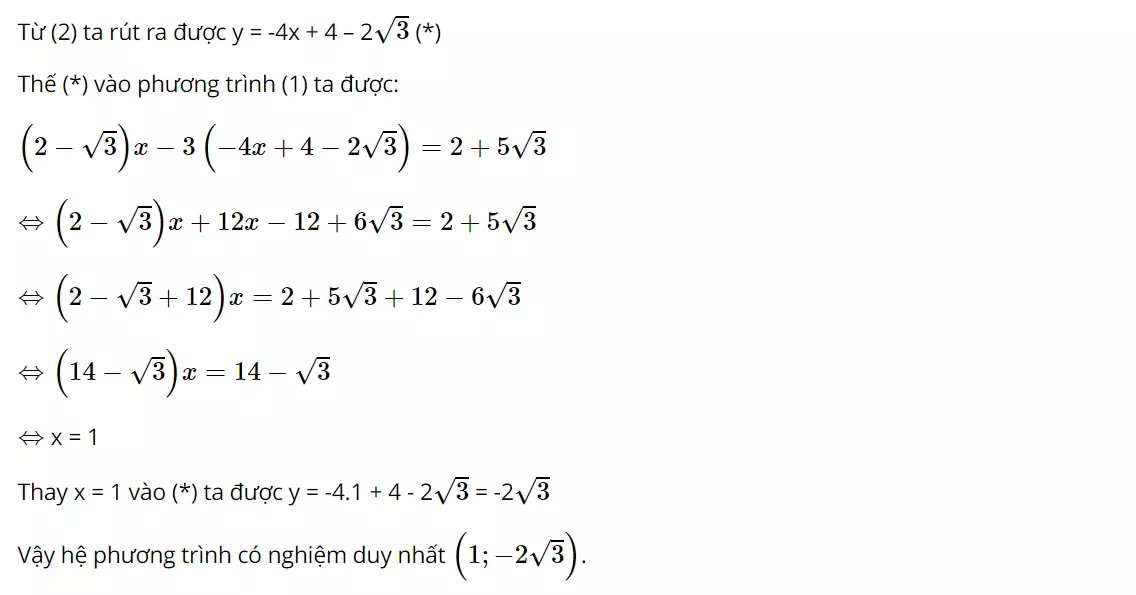
Bài 15 (trang 15 SGK Toán 9 Tập 2): Giải phương trình sau với các trường hợp: a) a = -1; b) a = 0; c) a = 1.
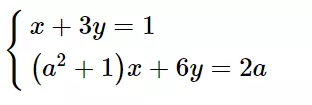
Hướng dẫn giải:
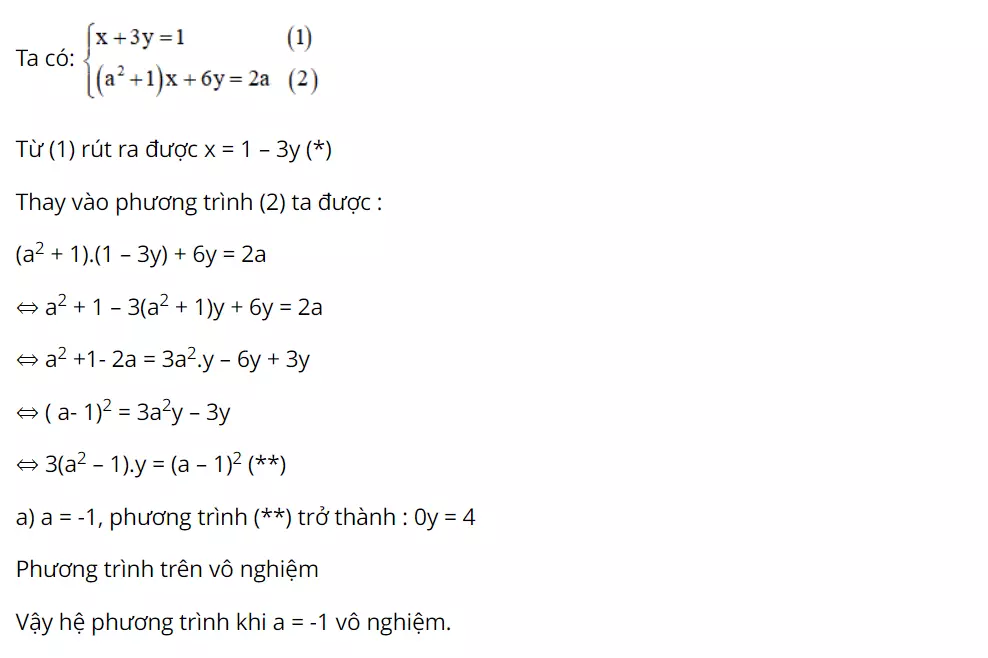
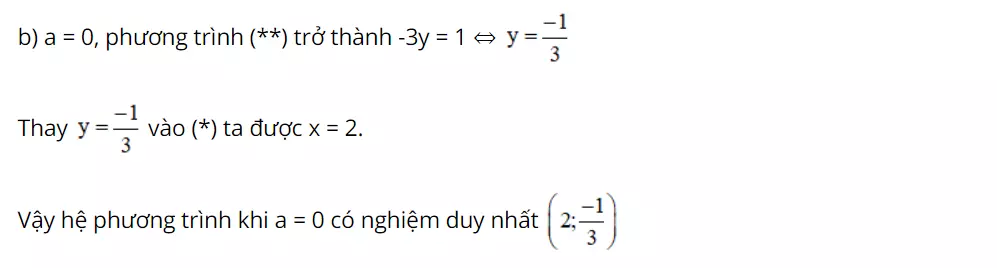

Trên đây là toàn bộ kiến thức cần nắm về giải hệ phương trình bằng phương pháp thế theo chương trình Toán lớp 9. Hy vọng bài viết sẽ giúp các em dễ dàng giải quyết các dạng bài tập và ôn thi học kỳ hay ôn thi vào 10 môn Toán.












