Hướng dẫn thuật toán sắp xếp Merge Sort trong lập trình C++

Chào mừng bạn đến với hướng dẫn về thuật toán sắp xếp Merge Sort trong lập trình C++. Merge Sort là một thuật toán sắp xếp độc đáo, với độ khó phức tạp trung bình và đạt được hiệu năng cao. Nếu bạn đang làm việc với các chương trình yêu cầu tối ưu, Merge Sort sẽ là lựa chọn tốt nhất. Hãy cùng tìm hiểu về Merge Sort và cách sử dụng nó trong ngôn ngữ C++.

Tìm hiểu thuật toán Merge Sort

Giống như thuật toán Quick Sort, Merge Sort cũng là một thuật toán được sử dụng để sắp xếp dãy số. Thuật toán này chia mảng cần sắp xếp thành hai nửa. Sau đó, tiếp tục chia nhỏ hai nửa mảng đã tạo ra và lặp lại quá trình này cho đến khi chỉ còn một phần tử trong mỗi mảng. Cuối cùng, chúng ta sẽ gộp hai nửa mảng đã tạo thành một mảng đã sắp xếp. Để gộp hai mảng này lại, chúng ta sử dụng hàm merge(). Hàm merge(arr, l, m, r) là bước quan trọng nhất để gộp hai mảng thành một mảng hoàn chỉnh.

Ví dụ về các bước của thuật toán Merge Sort

Nếu bạn chưa hiểu cách Merge Sort hoạt động, đừng lo lắng. Hãy xem ví dụ hình ảnh sau:

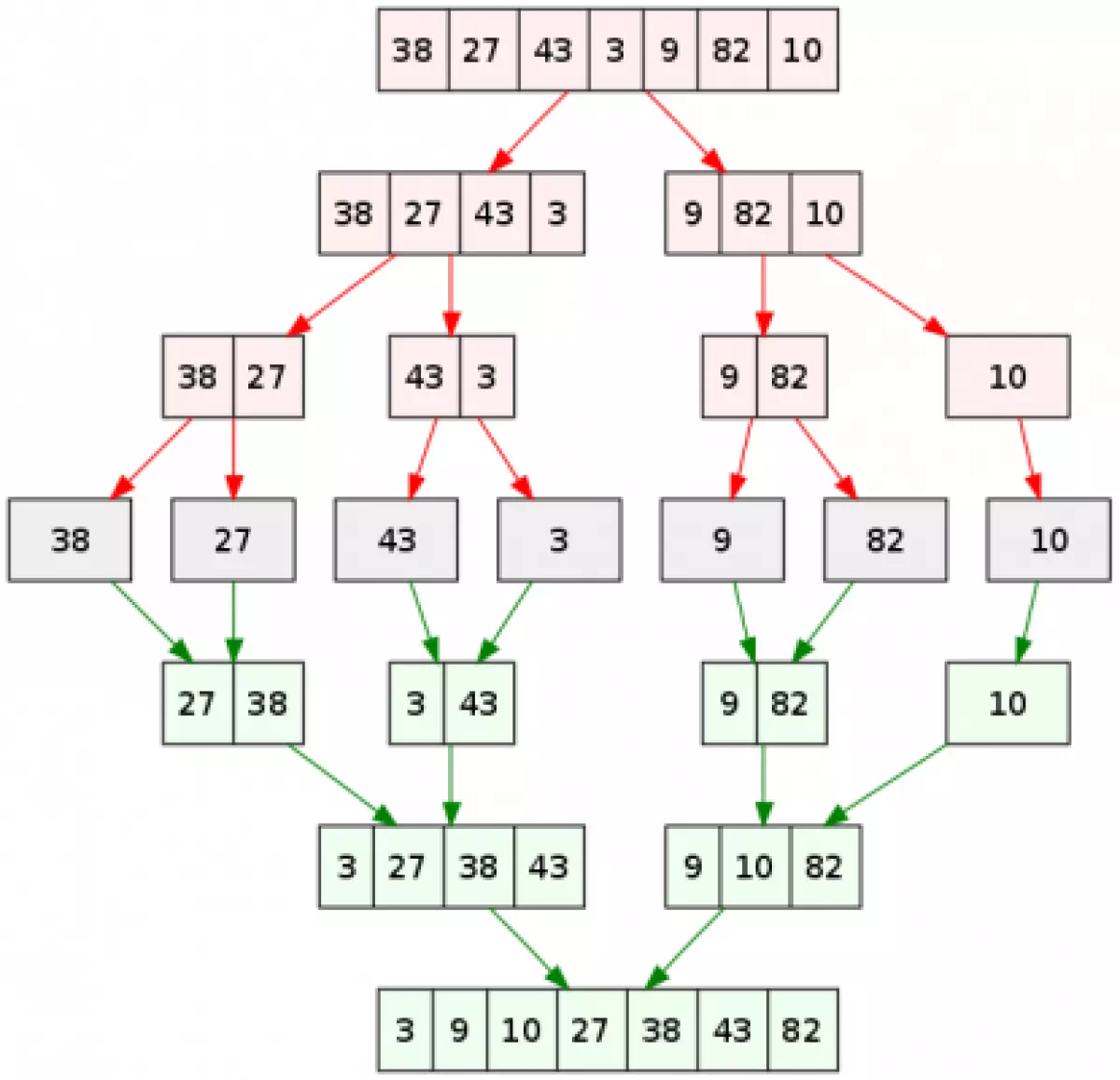Hình ảnh minh hoạ thuật toán Merge Sort

Hình ảnh trên là ví dụ về thuật toán Merge Sort cho mảng {38, 27, 43, 3, 9, 82, 10}. Nếu bạn xem kỹ hơn sơ đồ này, bạn sẽ thấy rằng mảng ban đầu đã được chia thành các mảng con nhỏ cho đến khi kích thước của mỗi mảng con là 1. Sau đó, chúng ta bắt đầu ghép các mảng con này lại với nhau cho đến khi có một mảng hoàn chỉnh theo thứ tự tăng dần.

1. Chúng ta có một mảng gốc là {38, 27, 43, 3, 9, 82, 10}.
2. Chia mảng gốc thành hai mảng con nhỏ hơn là arr1 = [38 27 43 3] , arr2 = [9 82 10].
3. Tiếp tục chia mảng arr1 và arr2 thành các mảng con nhỏ hơn.
4. Lặp lại quá trình trên cho đến khi các mảng con chỉ còn một phần tử duy nhất.
5. Bắt đầu ghép các mảng con lại với nhau sử dụng hàm Merge() theo thứ tự từ nhỏ đến lớn.
6. Cuối cùng, chúng ta có một mảng đã sắp xếp hoàn chỉnh là {3, 9, 10, 27, 38, 43, 82}.

Vậy hàm merge() là gì và có thể ghép các chuỗi theo thứ tự?

Dưới đây là một đoạn mã mẫu C++ mô tả thuật toán hàm merge và sắp xếp theo thuật toán Merge Sort:

#include 
#include 

// Gộp hai mảng con arr[l...m] và arr[m+1..r]
void merge(int arr[], int l, int m, int r) {
   int i, j, k;
   int n1 = m - l + 1;
   int n2 = r - m;

   /* Tạo các mảng tạm */
   int L[n1], R[n2];

   /* Copy dữ liệu sang các mảng tạm */
   for (i = 0; i < n1; i++)
      L[i] = arr[l + i];
   for (j = 0; j < n2; j++)
      R[j] = arr[m + 1+ j];

   /* Gộp hai mảng tạm vừa rồi vào mảng arr*/
   i = 0; // Khởi tạo chỉ số bắt đầu của mảng con đầu tiên
   j = 0; // Khởi tạo chỉ số bắt đầu của mảng con thứ hai
   k = l; // Khởi tạo chỉ số bắt đầu của mảng lưu kết quả
   while (i < n1 && j < n2) {
      if (L[i] <= R[j]) {
         arr[k] = L[i];
         i++;
      }
      else {
         arr[k] = R[j];
         j++;
      }
      k++;
   }

   /* Copy các phần tử còn lại của mảng L vào arr nếu có */
   while (i < n1) {
      arr[k] = L[i];
      i++;
      k++;
   }

   /* Copy các phần tử còn lại của mảng R vào arr nếu có */
   while (j < n2) {
      arr[k] = R[j];
      j++;
      k++;
   }
}

/* l là chỉ số trái và r là chỉ số phải của mảng cần được sắp xếp */
void mergeSort(int arr[], int l, int r) {
   if (l < r) {
      // Tương tự (l+r)/2, nhưng cách này tránh tràn số khi l và r lớn
      int m = l+(r-l)/2;

      // Gọi hàm đệ quy tiếp tục chia đôi từng nửa mảng
      mergeSort(arr, l, m);
      mergeSort(arr, m+1, r);

      // Gộp hai mảng con đã sắp xếp
      merge(arr, l, m, r);
   }
}

/* Hàm xuất mảng */
void printArray(int A[], int size) {
   int i;
   for (i=0; i < size; i++)
      printf("%d ", A[i]);
   printf("\n");
}

int main() {
   int arr[] = {12, 11, 13, 5, 6, 7};
   int arr_size = sizeof(arr)/sizeof(arr[0]);

   printf("Mảng ban đầu:\n");
   printArray(arr, arr_size);

   mergeSort(arr, 0, arr_size - 1);

   printf("Mảng đã sắp xếp:\n");
   printArray(arr, arr_size);

   return 0;
}

Ưu và nhược điểm của thuật toán Merge Sort:

• Ưu điểm: Merge Sort nhanh hơn các thuật toán cơ bản khác như Insertion Sort, Selection Sort và Interchage Sort. Nó cũng có thể nhanh hơn Quick Sort trong một số trường hợp.
• Nhược điểm: Thuật toán Merge Sort khó cài đặt và không thể nhận dạng được mảng đã được sắp xếp. Nó khá phức tạp so với các thuật toán sắp xếp khác.

Đó là những điều cần biết về thuật toán Merge Sort trong lập trình C++. Hy vọng rằng bài viết này đã giúp bạn hiểu rõ về thuật toán này và cách sử dụng nó trong công việc của mình. Hãy áp dụng Merge Sort vào các dự án của bạn để tối ưu hóa hiệu suất và đạt được kết quả tốt nhất.