Hướng dẫn tính nguyên hàm căn x và các bài tập minh hoạ dễ hiểu

Nguyên hàm là một khái niệm quan trọng trong toán học, và khi chúng ta nói về nguyên hàm của hàm số căn x, chúng ta đang xem xét cách tích hợp hàm này để tìm ra hàm gốc ban đầu. Trong bài viết này, chúng ta sẽ khám phá cách tính nguyên hàm căn x và cách ứng dụng nó trong nhiều vấn đề thú vị trong toán học và khoa học khác.

Các em có biết công thức ban đầu của căn bậc hai của x là gì không?

Công thức ban đầu của căn bậc hai của x là:

∫√x dx = (2/3)x^(3/2)C

Trong đó:

• C là hằng số tích phân.
• √x là căn bậc hai của x.
• x dx là nguyên hàm của căn bậc hai của x.

Để tính nguyên hàm của căn bậc hai của x, chúng ta sử dụng quy tắc nguyên tố của hàm số. Trong trường hợp này, chúng ta thấy rằng nguyên hàm của căn bậc hai của x là (2/3)x^(3/2) C, trong đó C là hằng số của phép cộng.

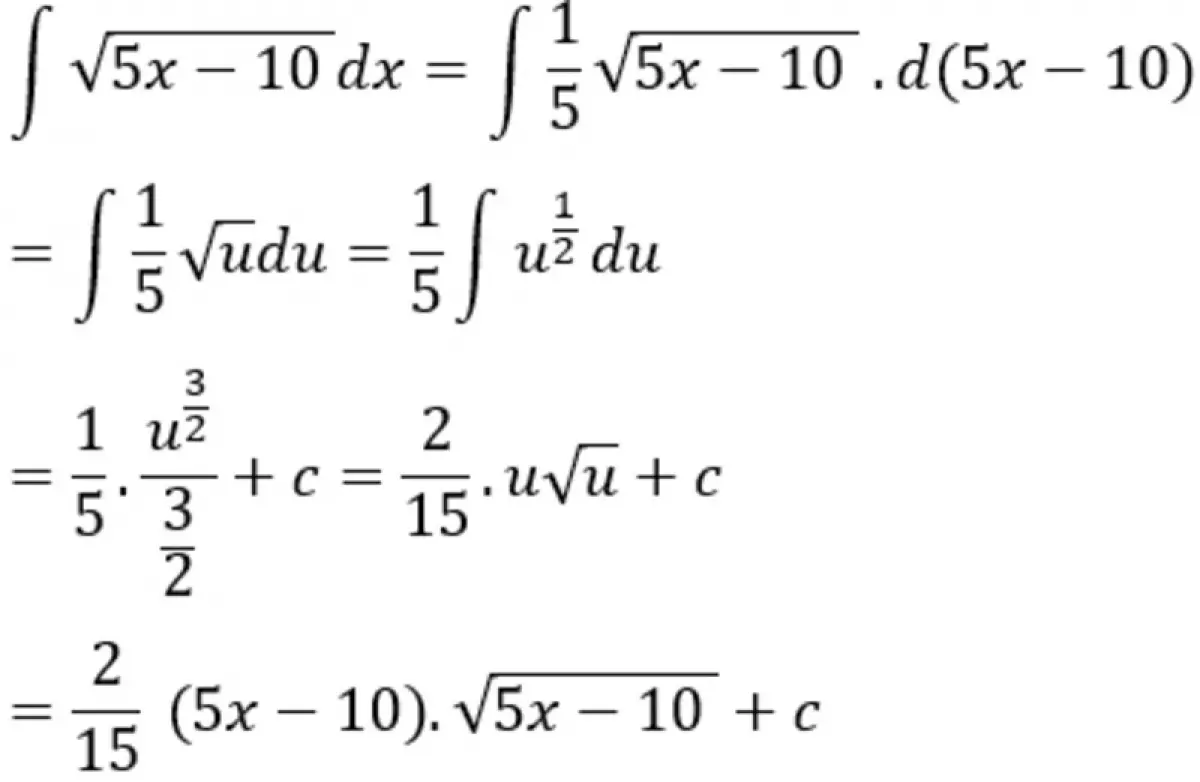Hình ảnh minh hoạ

Hướng dẫn tính căn bậc hai ban đầu của x

Để tính nguyên hàm của căn bậc hai của x, ta sử dụng quy tắc tính nguyên hàm của hàm căn bậc hai theo công thức:

∫√x dx = (2/3)x^(3/2)C

trong đó C là hằng số. Để tính nguyên hàm của căn bậc hai của x, chúng ta thay x bằng x^(1/2) trong công thức trên:

∫√(x^(1/2)) dx = (2/3)(x^(1/2 1/2 1)) C
= (2/3)(x^(3/2))C

Vậy nguyên hàm của căn bậc hai của x là (2/3)(x^(3/2)) C.

Tính giá trị căn bậc hai của x tại một điểm cho trước

Để tính toán giá trị của căn bậc hai của x tại một điểm cụ thể, chúng ta cần sử dụng công thức nguyên thủy của căn bậc hai. Công thức gốc của căn bậc hai của x có dạng sau:

∫√x dx = (2/3)√x^3 + C

Để tính giá trị của căn bậc hai của x tại một điểm xác định, ta thực hiện thay thế giá trị “x” trong công thức trên. Ví dụ, để tính giá trị căn bậc hai nguyên thủy của x tại điểm “x = 4,” ta thay thế giá trị “x=4” vào công thức:

∫√4 dx = (2/3)√4^3 + C

∫2 dx = (2/3)√64 + C

2x = 16/3 + C

Vậy, giá trị của căn bậc hai nguyên thủy của x tại điểm “x = 4” là “16/3 + C.”

Tính đạo hàm căn bậc hai của x

Trước hết, chúng ta xem xét công thức nguyên thủy ban đầu cho hàm số f(x) = √x

F(x) = (2/3)x^(3/2)C

Ở đây, C là một hằng số và x^(n/2) biểu thị căn bậc hai của x mũ n. Bây giờ, chúng ta sẽ tính đạo hàm của nguyên thủy này. Đạo hàm của hàm số f(x) = (2/3)x^(3/2) C là:

f'(x) = d/dx[(2/3)x^(3/2) C]
= (2/3) * (3/2) * x^(3/2 - 1)
= (2/3) * (3/2) * x^(1/2)
= x^(1/2)

Vậy kết quả là đạo hàm của căn bậc hai của x là x^(1/2).

Mối quan hệ giữa căn bậc hai nguyên thủy của x và hàm căn bậc hai của x là gì?

Căn bậc hai của x được biểu diễn bởi hàm F(x) mà thỏa mãn F′(x)=x​, với F′(x) là đạo hàm của F(x). Căn bậc hai của x cũng có thể được biểu diễn bằng hàm f(x)=x​. Mối quan hệ giữa chúng được thể hiện qua công thức sau: F(x)=32​x23​C, trong đó C là một hằng số.

Nghĩa là để tìm nguyên hàm căn bậc hai của x, chúng ta có thể tính dựa trên công thức F(x)=32​x23​C. Vì vậy, căn bậc hai nguyên thủy của x và hàm căn bậc hai của x có mối liên hệ với nhau thông qua việc sử dụng công thức này để tính toán.

Xem thêm:

• Đạo hàm arctan là gì? Công thức và quy tắc quan trọng cần nhớ
• Mẹo học công thức hạ bậc hay nhất