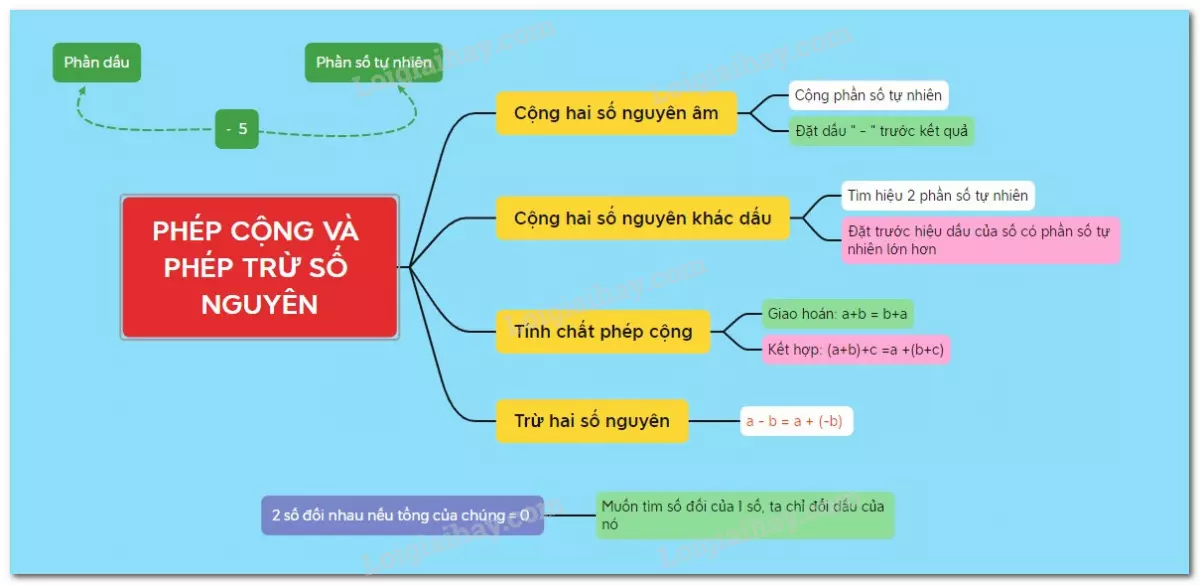
Cộng hai số nguyên cùng dấu
1. Phép cộng hai số nguyên dương
Cộng hai số nguyên dương chính là cộng hai số tự nhiên khác 0.
Ví dụ: (2 + 4 = 6).
2. Phép cộng hai số nguyên âm
Để cộng hai số nguyên âm, ta làm như sau:
Bước 1: Bỏ dấu "-" trước mỗi số.
Bước 2: Tính tổng của hai số nguyên dương nhận được ở Bước 1.
Bước 3: Thêm dấu "-" trước kết quả nhận được ở Bước 2, ta có tổng cần tìm.
Nhận xét:
-
Tổng của hai số nguyên dương là số nguyên dương.
-
Tổng của hai số nguyên âm là số nguyên âm.
Chú ý: Cho (a, b) là hai số nguyên dương, ta có:
(+a) + (+b) = a + b
(-a) + (-b) = -(a + b)Ví dụ:
(-3) + (-5) = -(3 + 5) = -8
(-13) + (-7) = -(13 + 7) = -20Cộng hai số nguyên khác dấu
Chú ý:
-
Tổng 2 số đối nhau bằng 0.
-
Số đối của một số nguyên dương là một số nguyên âm.
-
Số đối của một số nguyên âm là một số nguyên dương.
-
Số đối của (0) là (0).
Ví dụ:
-
Số đối của (3) là (-3).
-
Số đối của (-12) là (12).
-
Số đối của 2021 là (-2021).
- Quy tắc cộng hai số nguyên khác dấu:
Nhận xét: Hai số nguyên đối nhau có tổng bằng 0: (a + (-a) = 0).
Chú ý:
-
Nếu số dương lớn hơn số đối của số âm thì ta có tổng dương.
-
Nếu số dương bằng số đối của số âm thì ta có tổng bằng 0.
-
Nếu số dương bé hơn số đối của số âm thì ta có tổng âm.
Ví dụ:
a) (-8) + 2 = - (8 - 2) = -6
b) 17 + (-5) = 17 - 5 = 12
c) (-5) + 5 = 0 (Do (-5) và (5) là hai số đối nhau).
Tính chất của phép cộng các số nguyên
Ví dụ 1:
Tính một cách hợp lí: (-34) + (-15) + 34
Ta có:
(-34) + (-15) + 34
= (-15) + (-34) + 34 (Tính chất giao hoán)
= (-15) + [(-34) + 34] (Tính chất kết hợp)
= (-16) + 0 (cộng với số đối)
= -16 (cộng với số 0).
Ví dụ 2:
Trong một ngày, nhiệt độ ở Mát-xcơ-va lúc 5 giờ là (-7°C), đến 10 giờ tăng thêm (6°C) và lúc 12 giờ tăng thêm (4°C). Nhiệt độ ở Mát-xcơ-va lúc 12 giờ là bao nhiêu?
Giải
Nhiệt độ ở Mát-xcơ-va lúc 12 giờ là:
(-7) + 6 + 4 = (-7) + (6 + 4) = (-7) + 10 = 10 - 7 = 3°C.
IV. Phép trừ số nguyên
Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b:
a - b = a + (-b)
CÁC DẠNG TOÁN VỀ PHÉP CỘNG VÀ PHÉP TRỪ SỐ NGUYÊN
I. Thực hiện phép tính cộng, trừ hai số nguyên.
-
Nếu phép tính chỉ có phép cộng (phép trừ) thì ta sử dụng quy tắc cộng (trừ) hai số nguyên.
-
Nếu phép tính có nhiều hơn một phép cộng và phép trừ ta thực hiện theo thứ tự từ trái qua phải.
Ví dụ:
Tính (A = 15 - (-12) + 4)
Ta thấy trong biểu thức A có chứa nhiều hơn một phép cộng (trừ) => Ta thực hiện theo thứ tự từ trái qua phải. Do đó ta làm như sau:
A = 15 - (-12) + 4
= 15 + 12 + 4
= 27 + 4
= 31
Vậy (A = 31).
II. Bài toán tìm x trong phép cộng, trừ số nguyên
Dựa vào đề bài để áp dụng một trong các quy tắc sau:
-
Muốn tìm một số hạng trong một tổng ta lấy tổng trừ đi số hạng còn lại.
-
Muốn tìm số trừ ta lấy số bị trừ trừ đi hiệu.
-
Muốn tìm số bị trừ ta lấy hiệu cộng số trừ.
=> Kết luận.
Ví dụ:
Tìm (x), biết: (30 - x = 12)
Ta thấy trong phép trừ trên (x) là số trừ => Muốn tìm số trừ ta lấy số bị trừ (số 30) trừ đi hiệu (số 12). Do đó ta làm như sau:
30 - x = 12 x = 30 - 12 x = 18
Vậy (x = 18).
III. So sánh kết quả phép cộng, trừ hai số nguyên
Bước 1: Áp dụng quy tắc cộng, trừ số nguyên để thực hiện các phép tính
Bước 2: So sánh kết quả vừa tìm được ở bước 1
Bước 3: Kết luận
Ví dụ:
So sánh (A = -13 - (-34) + 25) và (B = -7 + 35 - 13)
Bước 1: A = -13 - (-34) + 25 A = -13 + 34 + 25 A = 21 + 25 A = 46
B = -7 + 35 - 13 B = 28 - 13 B = 15
Bước 2: Ta thấy (46 > 15) nên (A > B)
Bước 3: Vậy (A > B).
IV. Tính tổng (hiệu) nhiều số nguyên cho trước
Tùy đặc điểm từng bài, ta có thể giải theo các cách sau :
- Áp dụng tính chất giao hoán và kết hợp của phép cộng
- Cộng (trừ) dần hai số một
- Cộng các số dương với nhau, cộng các số âm với nhau, cuối cùng cộng các kết quả vừa tính được với nhau.
Ví dụ: Tính: (A = 5 + (-18) + 95 + (-82) + 100) A = 5 + (-18) + 95 + (-82) + 100 = (5 + 95) + [( -18) + (-82)] = 100 + ( -100) + 100 = 0 + 100 = 100
V. Bài toán liên quan đến phép cộng, trừ số nguyên
-
Bước 1: Căn cứ vào yêu cầu của đề bài suy luận để quy về phép cộng (trừ) hai số nguyên
-
Bước 2: Thực hiện phép tính
-
Bước 3: Kết luận.
Ví dụ: Nhiệt độ ở Sa Pa vào buổi trưa là (-2°C), đến tối nhiệt độ giảm (-4°C). Tính nhiệt độ buổi tối tại Sa Pa.
Do nhiệt độ buổi tối giảm (-4°C) so với buổi trưa nên ta sử dụng phép trừ
Do nhiệt độ buổi tối giảm (-4°C) so với buổi trưa nên ta có: (-2) - 4 = -2 - 4 = -6°C
Vậy nhiệt độ buổi tối tại Sa Pa là (-6°C).
VI. Tính giá trị biểu thức chứa phép cộng trừ các số nguyên tại một giá trị x cho trước
-
Bước 1: Thay giá trị của ẩn vào biểu thức
-
Bước 2: Áp dụng quy tắc cộng (trừ) hai số nguyên để thự hiện tính giá trị biểu thức.
-
Bước 3: Kết luận.
Ví dụ: Tính giá trị của (M = 12 - x) tại (x = 20)
Bước 1: Thay (x = 20) vào (M) ta được:
Bước 2: M = 12 - x M = 12 - 20 M = -8
Vậy tại (x = 20) thì (M = -8).
VII. Tính tổng tất cả các số nguyên thuộc khoảng cho trước
-
Bước 1: Liệt kê tất cả các số nguyên trong khoảng cho trước
-
Bước 2: Tính tổng tất cả các số nguyên đó, chú ý nhóm từng cặp số đối nhau bằng cách sử dụng tính chất giao hoán và kết hợp.
Ví dụ: Tính tổng các số nguyên thỏa mãn: (-5 < x ≤ 3)
Bước 1: Theo đề bài có (-5 < x ≤ 5) nên (x ∈ {-4, -3, -2, -1, 0, 1, 2, 3})
Bước 2: Ta có: (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 = (-4) + [(-3) + 3] + [(-2) + 2] + [(-1) + 1] + 0 = (-4) + 0 + 0 + 0 + 0 = -4