Theo định nghĩa của nguyên hàm, hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên đoạn K nếu F'(x) = f(x) với mọi x thuộc K. Đối với nguyên hàm căn x, biểu thức sẽ cung cấp giá trị của căn x, và để tìm giá trị x, chúng ta phải giải phương trình này.
Nguyên hàm của căn thức là một dạng toán khó giải nhất trong các dạng toán nguyên hàm. Dưới đây là một số công thức thường gặp từ cơ bản đến nâng cao:

Trong toán căn x nguyên hàm, chúng ta sẽ gặp một số dạng toán cơ bản. Dưới đây là ví dụ minh họa chi tiết:
Tìm nguyên hàm của hàm chứa căn thức bằng phương pháp đổi biến số
Cách tìm nguyên hàm, tích phân bằng phương pháp đổi biến:
- Cho hàm số u = u(x) có đạo hàm liên tục trên K và hàm số y = f(u) liên tục sao cho f[u(x)] xác định trên K. Khi đó nếu F là một nguyên hàm của f thì:
Ví dụ minh họa: Nguyên hàm của hàm số là:
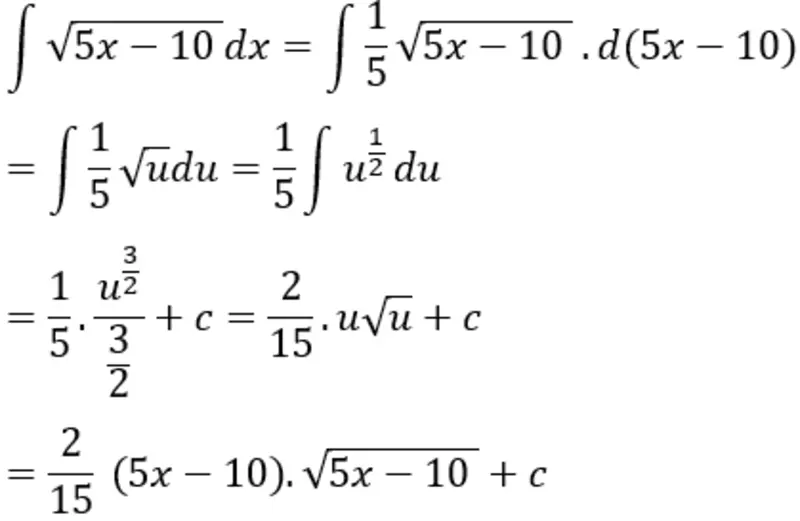
Lời giải: Ta có:
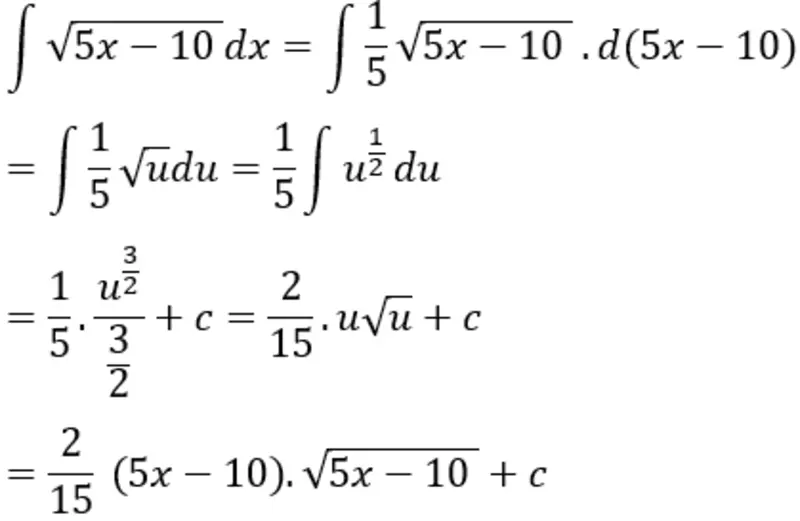
Đặt u = 5x - 10 ta được:
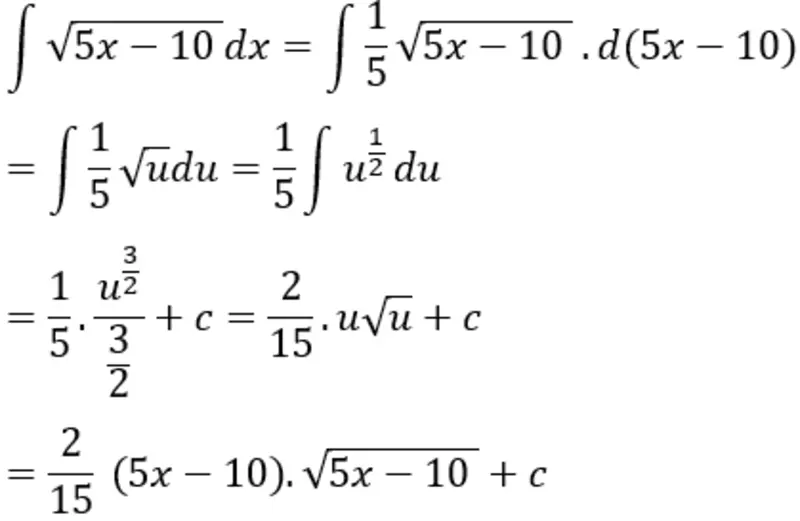
Chọn B.
Tìm nguyên hàm các hàm số chứa căn thức (hàm số vô tỉ) dựa trên tam thức bậc hai
Trên cơ sở đưa tam thức bậc hai về dạng chính tắc và dùng các công thức sau:

Ví dụ 1: Tìm nguyên hàm các hàm số chứa căn x sau:

Tìm nguyên hàm của hàm số f(x)=x - ax + a, với a > 0
Có hai cách để tìm nguyên hàm của hàm số này:

Các nguyên hàm I1 và I2 chúng ta đã biết cách giải.

Tìm nguyên hàm của hàm số f(x)=dxax + b +ax + c
Khử tính vô tỉ ở mẫu số bằng cách trục căn thức, ta được:
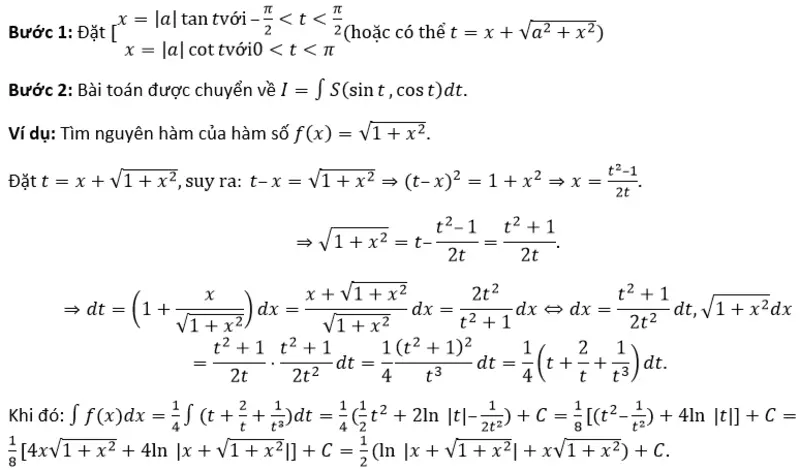
Tìm nguyên hàm của hàm số chứa căn thức (hàm số vô tỉ) bằng cách sử dụng các đồng nhất thức.
Ví dụ: Tìm nguyên hàm của hàm số: f(x)=xx+110
Tìm nguyên hàm của hàm số: f(x)=v(x)dxu2x ±a
Ta thực hiện theo các bước sau:
- Sử dụng phương pháp hằng số bất định ta xác định được a, b, c
- Áp dụng các công thức:
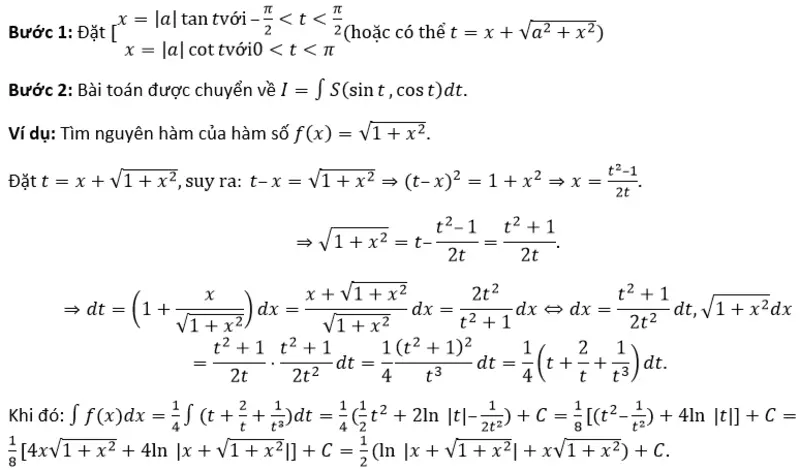
Tìm nguyên hàm của hàm số: I=∫R(x,a2+x2).dx
Ta thực hiện theo các bước sau:
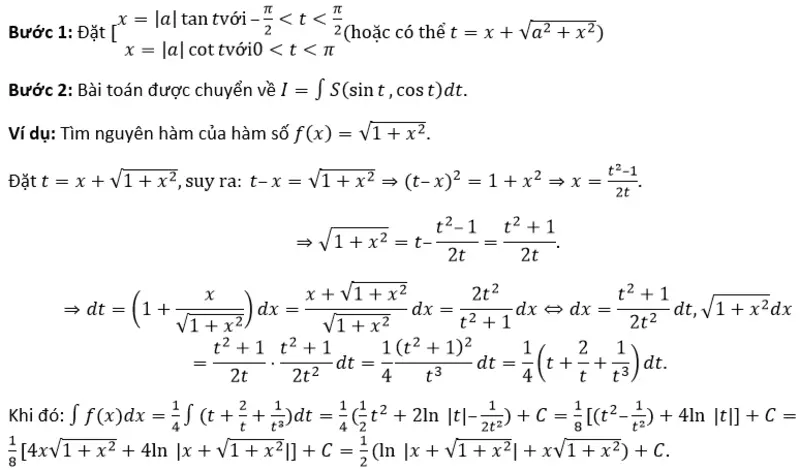
Tìm nguyên hàm của hàm số: I=∫R(x,x2-a2).dx
Ta thực hiện theo các bước sau:
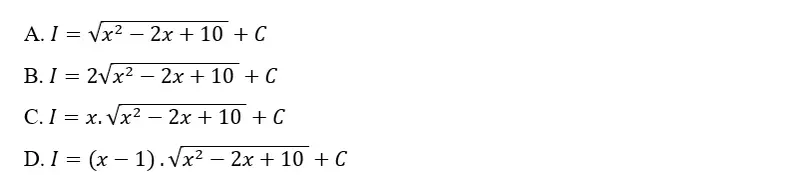
Để giúp học sinh học tập và luyện tập dạng toán nguyên hàm của căn x chi tiết hơn, dưới đây là một số dạng bài tập mà bạn có thể tham khảo và thực hành:
Bài tập 1: Tính nguyên hàm của hàm số sau:
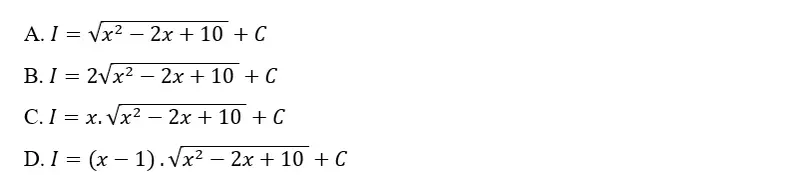
Lời giải:
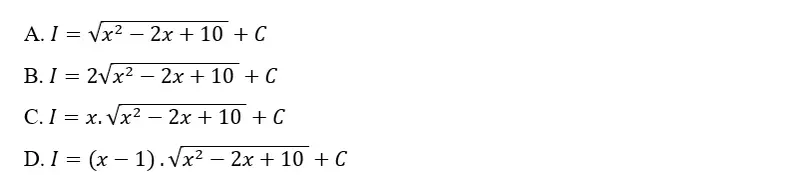
Bài tập 2: Tính nguyên hàm sau:
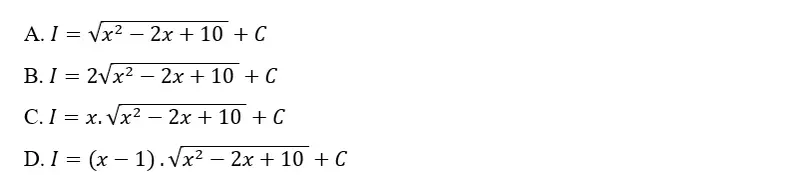
Lời giải:

Bài tập 3: Tính

Lời giải:

Bài tập 4: Tính nguyên hàm căn x của hàm số

Lời giải:
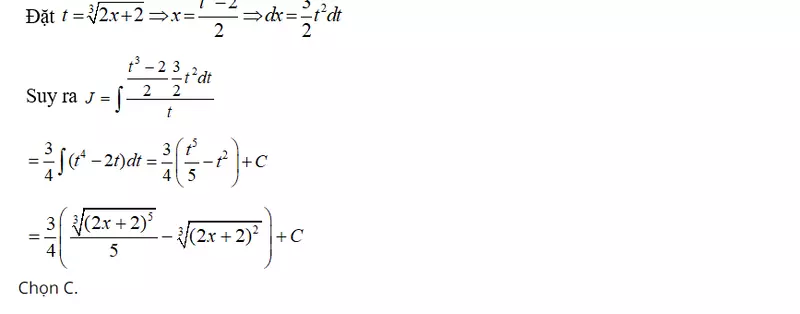
Bài tập 5 Tính
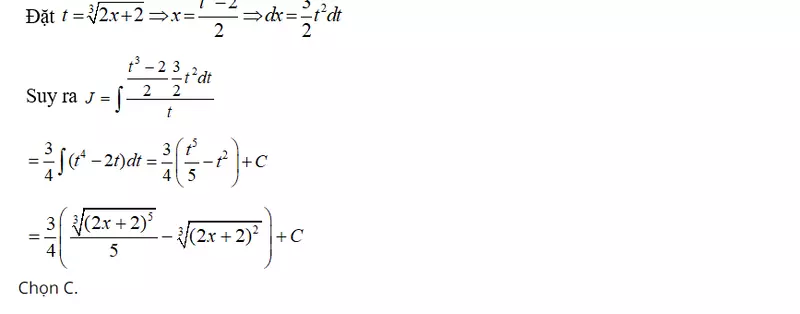
Lời giải:
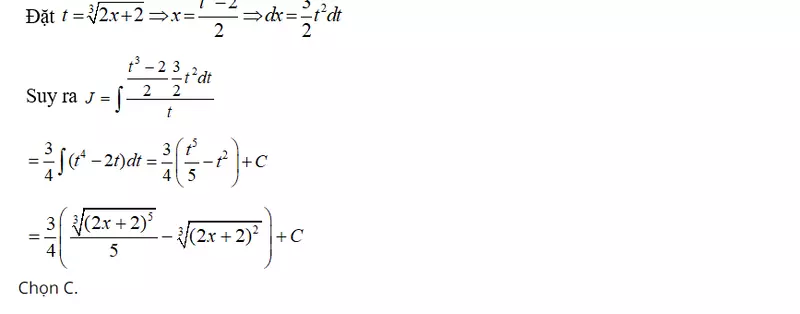
Trên đây là tổng hợp thông tin về dạng toán nguyên hàm căn x. Đây là một dạng toán nguyên hàm khá khó, nên khi học thì bạn cần nắm rõ công thức, các dạng toán và cách giải để có thể hoàn thành bài tập một cách chính xác nhất.












