Team4T's Coding Site: Hướng dẫn sử dụng thuật toán Dijkstra

Thuật toán Dijkstra là một trong những thuật toán cơ bản dùng để tìm đường đi ngắn nhất trong một đồ thị có trọng số không âm. Trong bài viết này, chúng ta sẽ tìm hiểu về thuật toán Dijkstra và cách sử dụng nó để giải quyết bài toán đường đi ngắn nhất từ một điểm tới mọi điểm còn lại trên đồ thị.

Sơ lược về thuật toán Dijkstra

Thuật toán Dijkstra hoạt động dựa trên nguyên tắc tham lam (greedy). Đầu tiên, chúng ta xây dựng một mảng chứa đường đi ngắn nhất từ điểm đang xét tới tất cả các điểm khác trên đồ thị, với giá trị ban đầu là vô cùng (+INF).

Quá trình thực hiện thuật toán Dijkstra diễn ra theo các bước sau:

1. Chọn một điểm chưa được duyệt và có đường đi ngắn nhất từ điểm gốc tới nó là nhỏ nhất.
2. Từ điểm đó, loang đường đi ra tất cả các đỉnh kề cận, và cập nhật lại đường đi ngắn nhất tới các đỉnh đó nếu đường đi mới tối ưu hơn.
3. Nếu còn điểm chưa được duyệt, ta quay lại bước 1.

Độ phức tạp không gian của thuật toán Dijkstra là O(V), với V là số đỉnh của đồ thị.

Thực hiện thuật toán Dijkstra trên đồ thị

Giả sử chúng ta có đồ thị vô hướng sau:

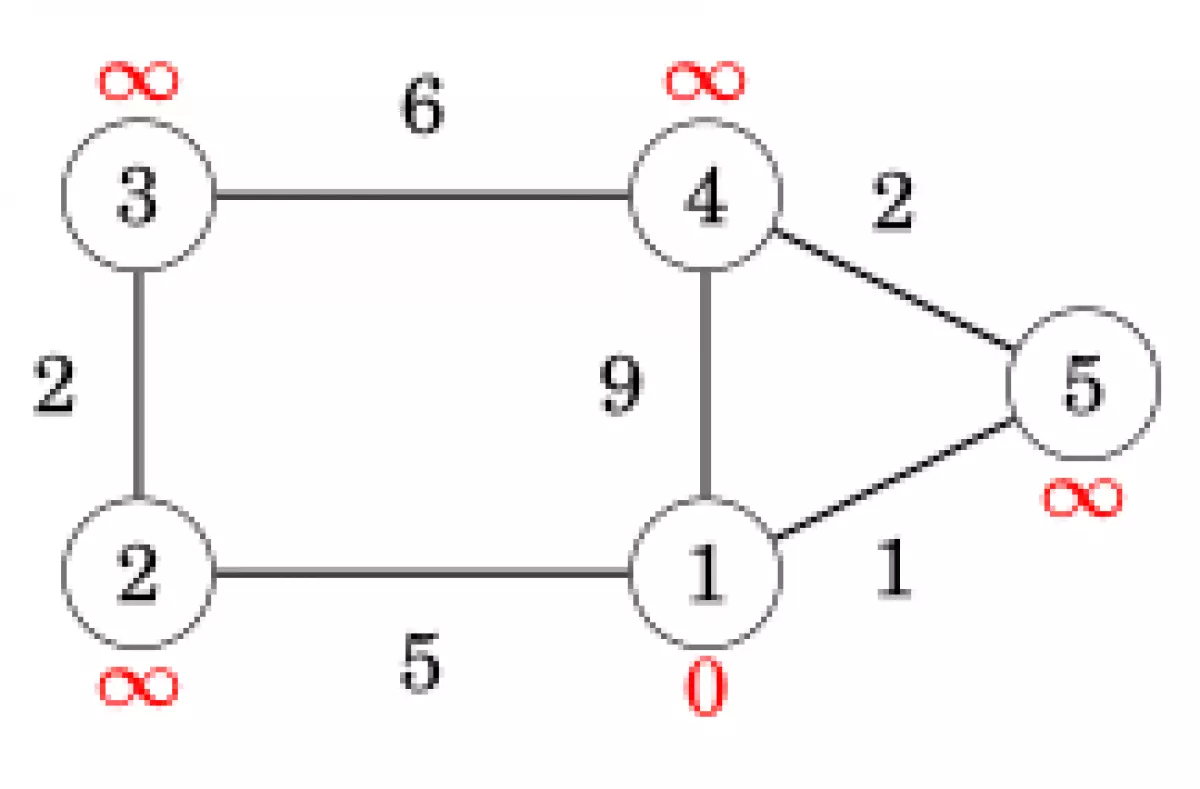
Chúng ta thực hiện thuật toán Dijkstra theo tuần tự các bước như sau:

1. Xét đỉnh 1 (đường đi ngắn nhất từ 1 tới 1 có độ dài là 0).
2. Sau quá trình cập nhật, chúng ta có các giá trị đường đi ngắn nhất mới:

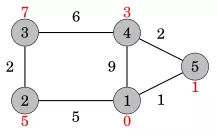
3. Tiếp theo, duyệt đỉnh 5 (đường đi ngắn nhất từ 1 tới 5 có độ dài 1).
4. Sau cập nhật, chúng ta thu được các giá trị mới:

5. Tiếp theo, duyệt đỉnh 4 (đường đi ngắn nhất từ 1 tới 4 có độ dài 3).
6. Sau cập nhật, chúng ta thu được các giá trị mới:

7. Tiếp tục quá trình trên cho đến khi duyệt hết tất cả các đỉnh, chúng ta sẽ có các giá trị đường đi ngắn nhất hoàn chỉnh:

Phương pháp tham lam của thuật toán Dijkstra đúng bởi chúng ta đã giả định trước đó rằng các trọng số của các cạnh không âm. Điều này đảm bảo rằng việc duyệt từ các đỉnh có đường đi ngắn nhất là cực tiểu là luôn chính xác. Chúng ta không thể đi qua một đỉnh khác để tìm một giá trị trung gian nhỏ hơn đường đi ngắn nhất từ điểm gốc tới một đỉnh cực tiểu.

Tuy nhiên, nếu trọng số âm xuất hiện, phương pháp tham lam này sẽ không còn đúng nữa. Ví dụ, xét đồ thị sau:

Bằng mắt thường, chúng ta có thể thấy rằng đường đi ngắn nhất từ đỉnh 1 tới đỉnh 4 sẽ là đoạn đường 1->3->4. Tuy nhiên, nếu áp dụng thuật toán Dijkstra, chúng ta sẽ có:

• Khởi tạo: s_path[1] = 0, s_path[2] = INF, s_path[3] = INF, s_path[4] = INF.
• Xuất phát từ đỉnh 1. Cập nhật: s_path[2] = 2, s_path[3] = 6.
• Xuất phát từ đỉnh 2. Cập nhật: s_path[4] = 5.
• Xuất phát từ đỉnh 4. Đây là đỉnh đích nên thuật toán kết thúc với kết quả ans = 5.

Rõ ràng, do phương pháp tham lam không xét đến trường hợp đường đi ngắn nhất có thể giảm, nên nhánh xuất phát từ đỉnh 3 bị loại bỏ, dẫn đến kết quả sai.

Cải tiến thuật toán Dijkstra

Độ phức tạp của quá trình tìm đỉnh tiếp theo để duyệt trong thuật toán Dijkstra quyết định đến hiệu suất của thuật toán. Với phương pháp tham lam cơ bản, quá trình này có độ phức tạp là O(V), với V là số đỉnh của đồ thị. Tuy nhiên, chúng ta có thể cải tiến quá trình này bằng cách sử dụng hàng đợi ưu tiên, từ đó giảm độ phức tạp của quá trình tìm kiếm đỉnh xuống cận theo hàm logarithm.

Một ví dụ về cách cài đặt thuật toán Dijkstra với hàng đợi ưu tiên như sau:

priority_queue> pq;
vector dist(N, INF); // Mảng chứa đường đi ngắn nhất từ điểm gốc tới các đỉnh khác
dist[1] = 0; // Đường đi ngắn nhất từ điểm gốc tới chính nó là 0
pq.push({0, 1});

while(!pq.empty()) {
    int u = pq.top().second;
    int d = -pq.top().first;
    pq.pop();

    if(d > dist[u]) continue; // Bỏ qua nếu đã tìm được đường đi ngắn nhất tới đỉnh u

    for(auto edge : graph[u]) {
        int v = edge.first;
        int w = edge.second;

        if(dist[u] + w < dist[v]) {
            dist[v] = dist[u] + w;
            pq.push({-dist[v], v});
        }
    }
}

Độ phức tạp của cách cài đặt trên là O(E+V*log V), với E là số cạnh và V là số đỉnh của đồ thị.

Bài toán tham khảo: Codeforces 20C - Dijkstra?

Bài toán này yêu cầu chúng ta tìm đường đi ngắn nhất từ đỉnh 1 tới đỉnh N trên một đồ thị vô hướng có trọng số. Nếu không có đường đi, chúng ta in ra -1. Nếu có nhiều đường đi cùng trả về một giá trị tối ưu, chúng ta có thể tùy chọn đường đi.

Đây là một bài tập cơ bản để áp dụng thuật toán Dijkstra. Để giải quyết bài toán này, chúng ta cần lưu ý các điểm sau:

• Output sẽ trả về -1 nếu sau khi kết thúc duyệt, không tồn tại đường đi từ điểm 1 tới điểm N (đồ thị không đảm bảo liên thông).
• Ngoài việc xác định giá trị đường đi ngắn nhất, chúng ta còn cần thực hiện truy vết để in ra đường đi. Phương pháp truy vết tương tự với khi duyệt BFS hoặc DFS thông thường.

Một ví dụ lời giải cho bài toán này có thể được tìm thấy tại Submission 33253245.

Kết luận

Trên đây là một hướng dẫn sơ lược về thuật toán Dijkstra và cách sử dụng nó để giải quyết bài toán đường đi ngắn nhất trên một đồ thị. Hy vọng rằng thông qua bài viết này, bạn đã có được hiểu biết căn bản về thuật toán Dijkstra và có thể áp dụng nó vào các bài toán thực tế khác.

Nguồn tham khảo: Sách Competitive Programming’s Handbook của Antti Laaksonen, CSES (Phần Lan).