Trong toán học, phép tích vectơ, nhân vectơ hay tích có hướng là một phép toán nhị nguyên trên các vectơ trong không gian vectơ ba chiều. Đây là một trong hai phép nhân thường gặp giữa các vectơ, với phép toán kia là nhân vô hướng. Tích vectơ khác với nhân vô hướng bởi vì kết quả thu được là một giả vectơ thay vì một vô hướng. Kết quả này vuông góc với mặt phẳng chứa hai vectơ đầu vào của phép nhân.
Định nghĩa
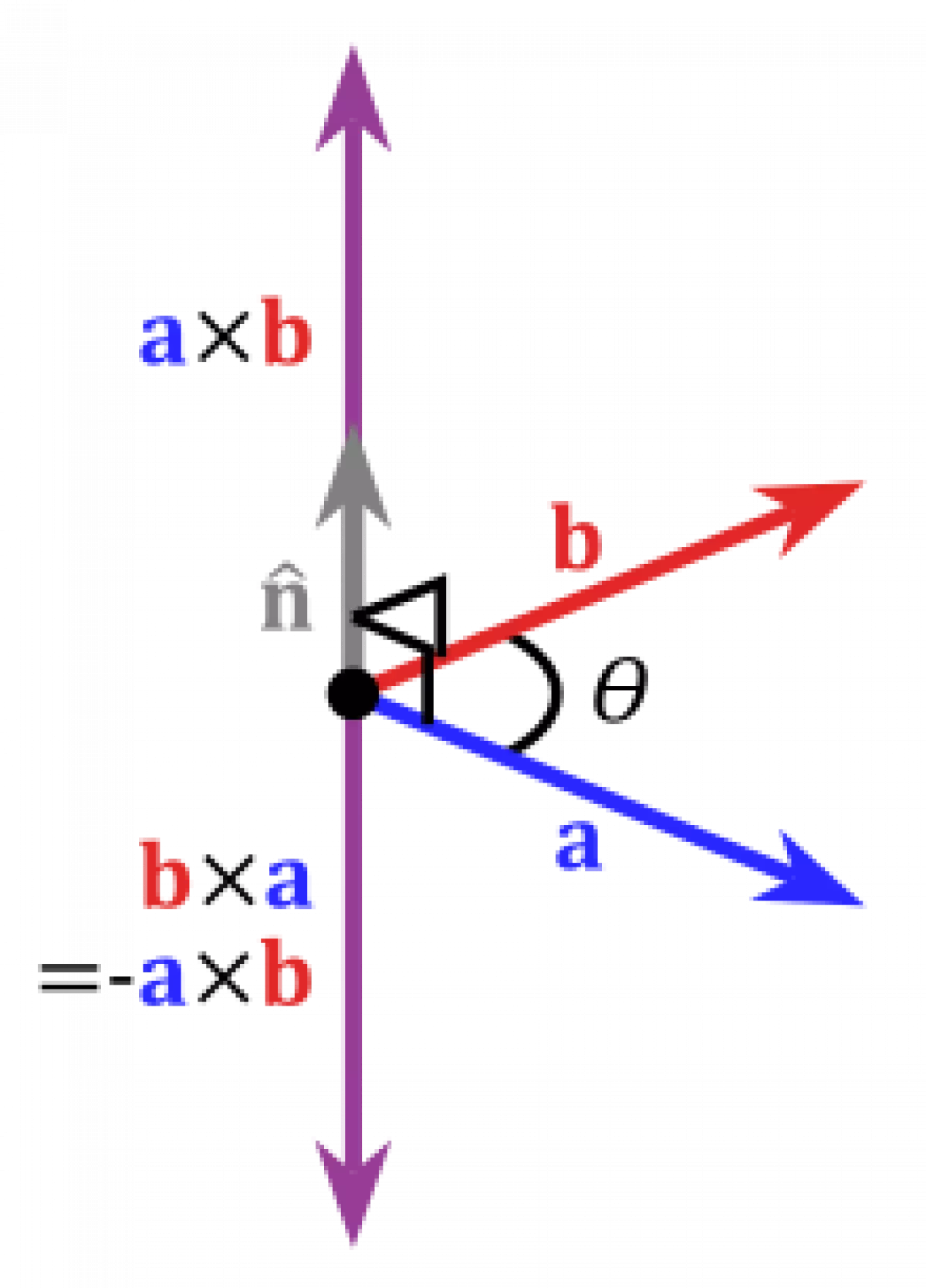
Phép nhân vectơ của vectơ a và b được ký hiệu là a × b hay [a, b], định nghĩa bởi: a × b = n |a| |b| sin θ với θ là góc giữa a và b (0° ≤ θ ≤ 180°) nằm trên mặt phẳng chứa a và b, và n là vectơ đơn vị vuông góc với a và b.
Thực tế có hai vectơ n thỏa mãn điều kiện vuông góc với a và b (khi a và b không cùng phương), vì nếu n vuông góc với a và b thì -n cũng vậy.
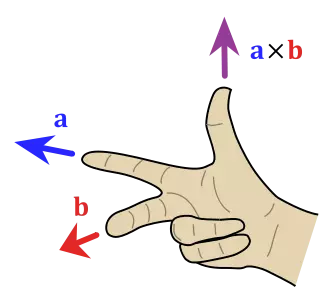
Việc chọn hướng của vectơ n phụ thuộc vào hệ tọa độ tuân theo quy tắc bàn tay trái hay quy tắc bàn tay phải. (a, b, a × b) tuân cùng quy tắc với hệ tọa độ đang sử dụng để xác định các vectơ.
Vì kết quả phụ thuộc vào quy ước hệ tọa độ, nó được gọi là giả vectơ. May mắn là trong các hiện tượng tự nhiên, nhân vectơ luôn đi theo cặp đối chiều nhau, nên kết quả cuối cùng không phụ thuộc lựa chọn hệ tọa độ.
Tính chất
Phép tính này phản giao hoán: a × b = -(b × a)
Nó phân phối được trên phép cộng vectơ: a × (b + c) = a × b + a × c
Nó kết hợp được với nhân vô hướng: (r⋅a) × b = a × (r⋅b) = r⋅(a × b), với "." chỉ nhân vô hướng.
Nó không có tính kết hợp, (a × b) × c ≠ (a × b) × c
Nó thỏa mãn đẳng thức Jacobi: a × (b × c) + b × (c × a) + c × (a × b) = 0.
2 vectơ không cùng phương thì tích có hướng là một vectơ vuông góc với 2 vectơ đã cho.
Các tính chất trên cho thấy không gian vectơ ba chiều với phép nhân vectơ tạo thành một đại số Lie.
Tích có hướng trong hệ tọa độ Descartes
Trong không gian với hệ trục tọa độ Oxyz, cho n₁ = (A₁, B₁, C₁) và n₂ = (A₂, B₂, C₂), khi đó tích có hướng giữa 2 vectơ là vectơ có tọa độ [n₁, n₂] = (| B₁ C₁ B₂ C₂ |, | C₁ A₁ C₂ A₂ |, | A₁ B₁ A₂ B₂ |)
Ứng dụng
Ý nghĩa hình học
Nhiều công thức tính trong không gian vectơ ba chiều liên quan đến nhân vectơ, nhờ vào kết quả là vectơ vuông góc với hai vectơ đầu vào.
- Diện tích hình bình hành ABCD: S = | [AB; AD] | = AB ⋅ AD ⋅ sin(A)
- Thể tích khối hộp ABCDA'B'C'D': V = | [AB; AD] ⋅ AA' |
- 2 vectơ u và v cùng phương ⇔ [u; v] = 0
- 3 vectơ u, v, w đồng phẳng ⇔ [u; v] ⋅ w = 0
Ứng dụng trong vật lý
Phép tính này xuất hiện ở công thức tính lực Lorentz do một trường điện từ tác động lên một điện tích. Công thức tính mômen lực hay mômen động lượng cũng liên quan đến nhân vectơ.
Xem thêm
- Quy tắc bàn tay phải
Tham khảo
- Tích vectơ trên Từ điển bách khoa Việt Nam













