1. Lý thuyết các phép toán tập hợp
1.1. Phép hợp
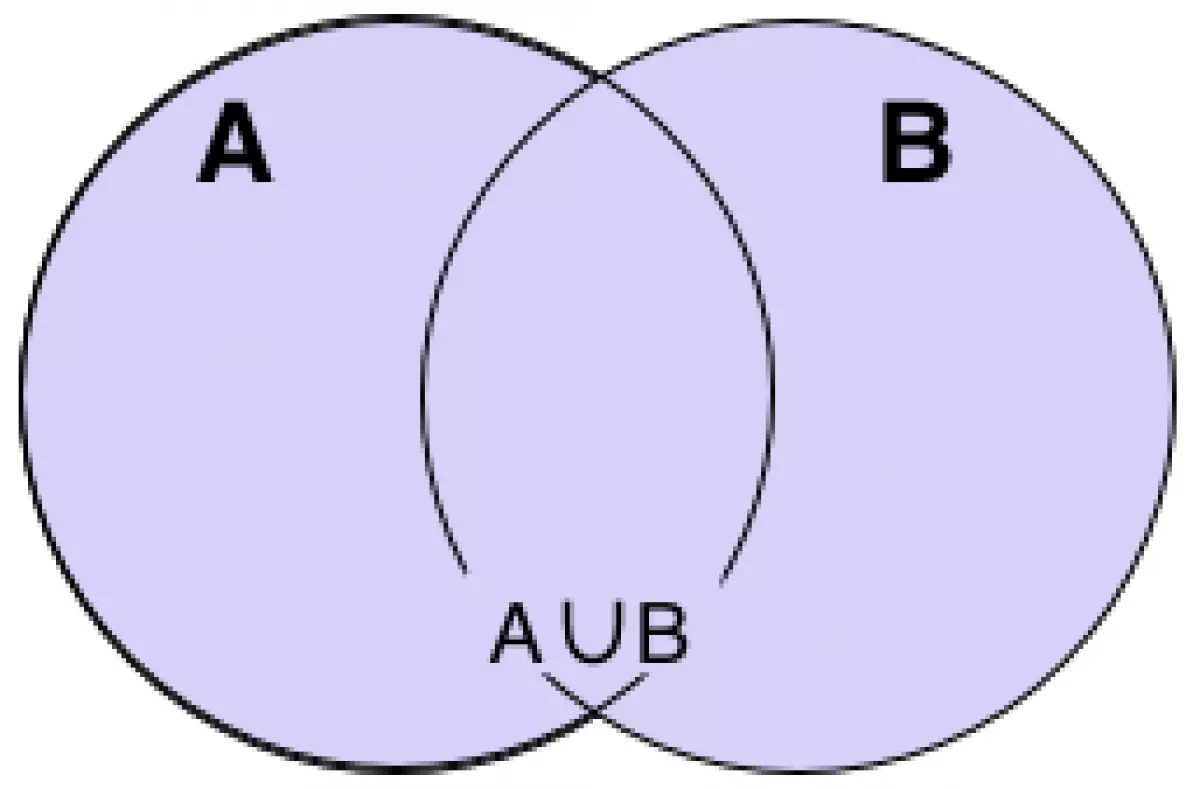
Hợp của hai tập hợp A và B là tập hợp bao gồm tất cả các phần tử thuộc A hoặc thuộc B. Ký hiệu là A∪B.
A∩B⇔{x∣ x∈A và x∈B}
Ví dụ: Cho tập A={2;3;4},B={1;2} thì A∪B={1;2;3;4}
1.2. Phép giao
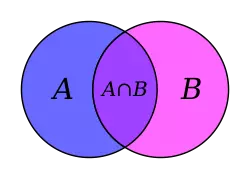
Giao của hai tập hợp A, B là tập hợp bao gồm tất cả các phần tử thuộc cả A và B. Kí hiệu là A∩B.
A∪B ⇔ {x∣x∈A hoặc x∈B}
Nếu 2 tập hợp A, B không có phần tử chung, A∩B=∅ khi đó ta gọi A và B là 2 tập hợp rời nhau.
Ví dụ: Cho tập A={2;3;4},B={1;2} thi A∩B={1}
1.3. Phép hiệu
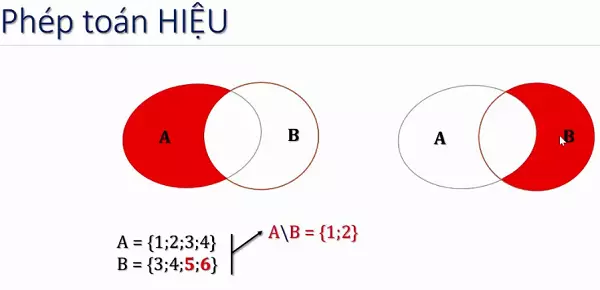
Hiệu của tập hợp A, B là tập hợp tất cả các phần tử thuộc A nhưng lại không thuộc B. Ký hiệu: A∖B
A∖B= x∣x∈A & x∉B
Ví dụ: Cho tập A = {2;3;4}, B = {1;2} ta có:
A∖B = {3;4}
B∖A = {1}
1.4. Phần bù
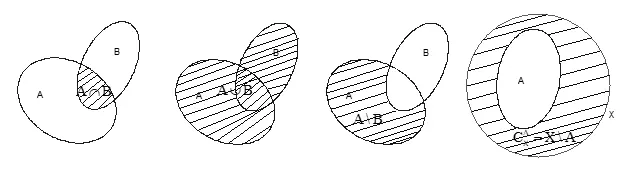
Ta có A là tập con của E. Phần bù A trong X là X∖A, ký hiệu (CXA) là tập hợp cả các phần tử của E mà không là phần tử của A.
Ví dụ: Cho tập A = {2;3;4},B={1;2} ta có CAB=A∖B={3;4}
2. Một số bài tập về các phép toán tập hợp và phương pháp giải
Phương pháp giải chung:
- Hợp của 2 tập hợp
x ∈ A ∪ B ⇔ x ∈ A hoặc x ∈ B
- Giao của 2 tập hợp
x ∈ A ∩ B ⇔ x ∈ A hoặc x ∈ B
- Hiệu của 2 tập hợp
x ∈ A ∖ B ⇔ x ∈ A hoặc x ∉ B
- Phần bù
Khi B ⊂ A thì AB là phần bù của B trong A (kí hiệu là CAB)
Ví dụ 1: Cho A là tập hợp học sinh lớp 10 đang học ở trường và B là tập hợp các học sinh đang học Tiếng Anh của trường. Hãy diễn đạt bằng lời các tập hợp sau: A∪B; A∩B; A∖B; B∖A.
Giải:
-
A ∪ B: tập hợp các học sinh hoặc học lớp 10 hoặc học môn Tiếng Anh của trường.
-
A ∩ B: tập hợp học sinh lớp 10 học môn Tiếng Anh của trường.
-
A∖B: tập hợp các học sinh học lớp 10 nhưng không học môn Tiếng Anh của trường.
-
B∖A: tập hợp các học sinh học môn Tiếng Anh của trường em nhưng không học lớp 10 của trường.
Ví dụ 2: Cho A={1,2,3,4,5,6,9}; B={1,2,4,6,8,9} và C={3,4,5,6,7}
a) Tìm hai tập hợp (A∖B) ∪ (B∖A) và (A∪B) \ (A∩B). Hai tập hợp nhận được có bằng nhau hay không?
b) Hãy tìm A∩(B∖C) và (A∩B)∖C. Hai tập hợp nhận được có bằng nhau hay không?
Giải
a) A∖B={3,5}; B∖A={8}
⇒ (A∖B) ∪ (B∖A)={3,5,8}
A∪B={1,2,3,4,5,6,8,9}
A∩B={1,2,4,6,9}
⇒ (A∪B) \ (A∩B)={3,5,8}
Do đó: (A∖B) ∪ (B∖A)=(A∪B) \ (A∩B)
b) B∖C={1,2,8,9}
⇒ A∩(B∖C)={1,2,9}.
A∩B={1,2,4,6,9}
⇒ (A∩B)∖C={1,2,9}.
Do đó: A∩(B∖C)=(A∩B)∖C
Ví dụ 3: Viết mỗi tập hợp sau bằng cách chỉ ra tính chất đặc trưng cho các phần tử của nó:
a) A = {2; 3; 5; 7}
b) B = {-3; -2; -1; 0; 1; 2; 3}
c) C = {-5; 0; 5; 10; 15}.
Giải:
a) A là tập hợp các số nguyên tố nhỏ hơn 10.
b) B là tập hợp các số nguyên có giá trị tuyệt đối không vượt quá 3.
B={x ∈ Z||x| ≤ 3}.
c) C là tập hợp các số nguyên n chia hết cho 5, không nhỏ hơn -5 và không lớn hơn 15.
C={n ∈ Z|-5 ≤ n ≤ 15; n ⋮ 5}
3. 10 câu hỏi trắc nghiệm các phép toán tập hợp có đáp án
Câu 1: Cho các tập hợp A = {m ∈ N | m là ước của 16}; B = {n ∈ N | n là ước của 24}.
Tập hợp A ∩ B là:
A. ∅
B. {1; 2; 4; 8}
C. {±1; ±2; ±4; ±8}
D. {1; 2; 4; 8; 16}
Giải:
Ta có A = {m ∈ N | m là ước của 16} = {1; 2; 4; 8; 16}.
B = {n ∈ N | n là ước của 24 = {1; 2; 3; 4; 6; 8; 12; 24}.
⇒ A ∩ B = {1; 2; 4; 8}.
Chú ý: A ∩ B chính là tập hợp các ước số tự nhiên của 8 = ƯCLN(16;24).
Chọn đáp án B
Câu 2: Xác định tập hợp X thỏa mãn hai điều kiện:
X ∪ {1; 2; 3} = {1; 2; 3; 4} và X ∩ {1; 2; 3; a} = {2; 3}.
A. X = {2; 3}
B. X = {1; 2; 3; 4}
C. X = {2; 3; 4}
D. X = {2; 3; 4; a}
Giải:
Chọn đáp án C
Vì X ∪ {1; 2; 3} = {1; 2; 3; 4} nên 4 ∈ X và tập X ⊂ {1; 2; 3; 4}. Vì X ∩ {1; 2; 3; a} = {2; 3} nên 2; 3 ∈ X và 1 ∉ X, a ∉ X.
Tóm lại, ta có X = {2; 3; 4}.
Câu 3: Cho A = {a, b, c, d, e} và B = {c, d, e, k}. Tập hợp A ∩ B là:
A. {a, b}
B. {c, d, e}
C. {a, b, c, d, e, k}
D. {a, b, k}
Giải:
Chọn đáp án B
A= {a; b; c; d;e} và B= {c; d; e; k}
Tập hợp A ∩ B= {c; d;e}
Conclusion
Với kiến thức về phép hợp, phép giao, phép hiệu và phần bù trong các phép toán tập hợp, các em đã có thể giải các bài tập liên quan đến phép toán tập hợp một cách thành thạo. Hy vọng qua bài viết này, các em đã nắm được những điểm quan trọng để áp dụng vào việc học và giải quyết các bài toán thực tế. Nếu có bất kỳ thắc mắc nào hoặc muốn tìm hiểu thêm, hãy truy cập ngay Vuihoc.vn để đăng ký tài khoản hoặc liên hệ trung tâm hỗ trợ để có được sự hỗ trợ tốt nhất. Chúc các em thành công trong việc học tập và làm bài tập!












