Giới Thiệu
Bạn đã bao giờ tự hỏi làm thế nào máy tính có thể sắp xếp một lượng lớn dữ liệu một cách nhanh chóng? Câu trả lời nằm ở thuật toán sắp xếp.
Trong thế giới lập trình, thuật toán sắp xếp đóng vai trò vô cùng quan trọng. Nó là nền tảng cho nhiều giải thuật phức tạp hơn, giúp tối ưu hóa hiệu suất xử lý dữ liệu. Hãy tưởng tượng việc tìm kiếm thông tin trong một danh sách lộn xộn và một danh sách được sắp xếp gọn gàng, bạn sẽ thấy sự khác biệt rõ ràng.
Bài viết này sẽ dẫn dắt bạn vào thế giới của 7 thuật toán sắp xếp phổ biến trong C++, từ đơn giản đến phức tạp. Mỗi thuật toán sẽ được giải thích cặn kẽ về ý tưởng, cách thức hoạt động và cả đoạn code minh họa.
Hãy cùng khám phá!
Các Thuật Toán Sắp Xếp Cơ Bản
1. Sắp Xếp Nổi Bọt (Bubble Sort)
Bubble Sort, hay còn gọi là sắp xếp nổi bọt, là thuật toán đơn giản nhất. Nó hoạt động bằng cách so sánh hai phần tử liền kề và đổi chỗ chúng nếu chúng không theo thứ tự mong muốn. Quá trình này được lặp đi lặp lại cho đến khi toàn bộ danh sách được sắp xếp.
Ưu điểm:
- Dễ hiểu và dễ cài đặt.
Nhược điểm:
- Hiệu suất thấp với danh sách lớn, độ phức tạp thời gian là O(n^2).
2. Sắp Xếp Chọn (Selection Sort)

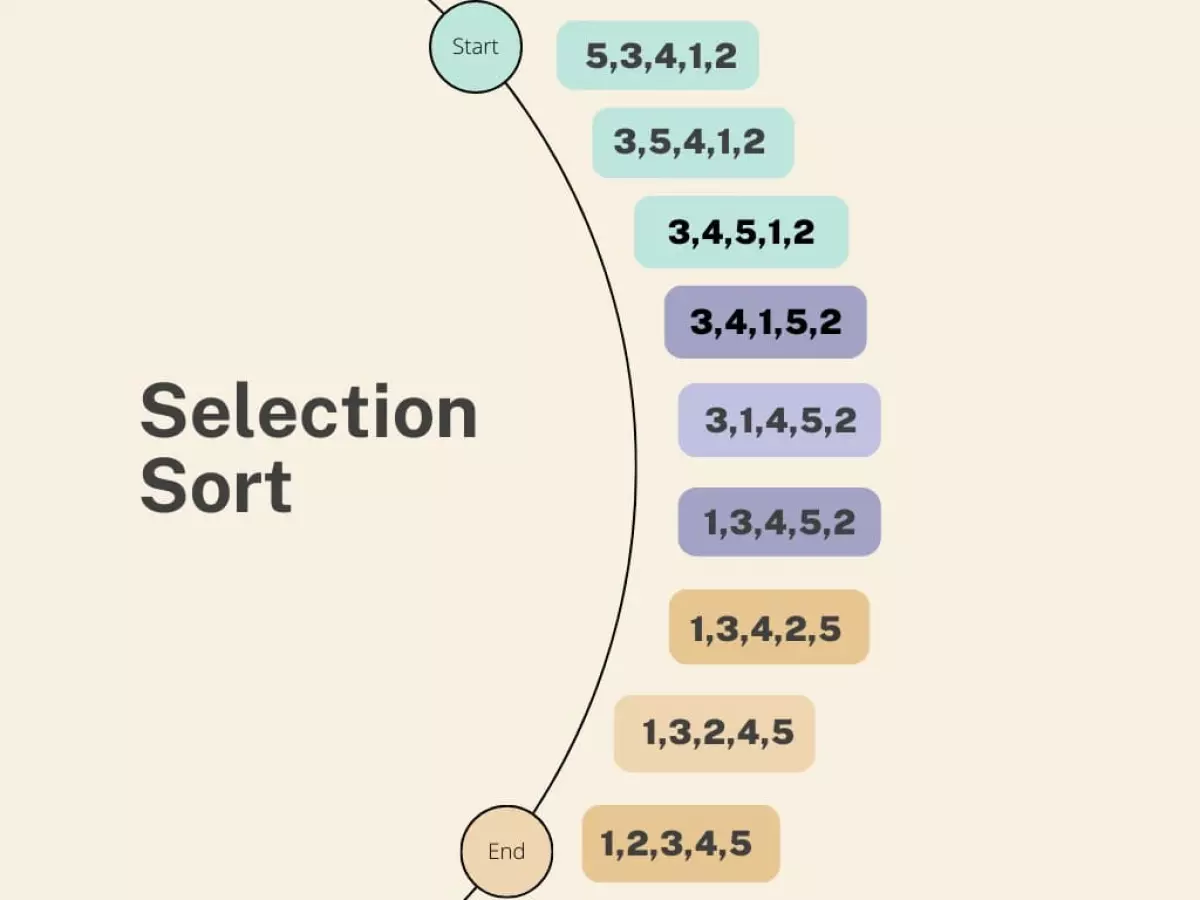
Selection Sort hoạt động bằng cách tìm kiếm phần tử nhỏ nhất (hoặc lớn nhất) trong danh sách và đổi chỗ nó với phần tử đầu tiên. Quá trình này được lặp lại cho phần còn lại của danh sách cho đến khi toàn bộ danh sách được sắp xếp.
Ưu điểm:
- Dễ hiểu và dễ cài đặt.
Nhược điểm:
- Hiệu suất thấp với danh sách lớn, độ phức tạp thời gian là O(n^2).
3. Sắp Xếp Chèn (Insertion Sort)
Insertion Sort hoạt động giống như cách chúng ta sắp xếp bài khi chơi bài. Nó duyệt qua danh sách, lấy từng phần tử và chèn nó vào vị trí thích hợp trong phần đã được sắp xếp của danh sách.
Ưu điểm:
- Hiệu quả với danh sách nhỏ hoặc danh sách gần như đã được sắp xếp.
Nhược điểm:
- Hiệu suất giảm khi kích thước danh sách tăng, độ phức tạp thời gian trong trường hợp xấu nhất là O(n^2).
Các Thuật Toán Sắp Xếp Nâng Cao
4. Sắp Xếp Nhanh (Quick Sort)
Quick Sort là một thuật toán chia để trị, hoạt động bằng cách chọn một phần tử làm "chốt" và chia danh sách thành hai phần: phần tử nhỏ hơn chốt và phần tử lớn hơn chốt. Sau đó, nó sắp xếp đệ quy hai phần này.
Ưu điểm:
- Hiệu suất trung bình rất tốt, độ phức tạp thời gian trung bình là O(n log n).
Nhược điểm:
- Hiệu suất kém trong trường hợp xấu nhất, có thể đạt đến O(n^2).
5. Sắp Xếp Trộn (Merge Sort)
Merge Sort cũng là một thuật toán chia để trị. Nó chia danh sách thành các nửa nhỏ hơn cho đến khi mỗi nửa chỉ chứa một phần tử. Sau đó, nó hợp nhất các nửa này theo thứ tự đã sắp xếp cho đến khi có được danh sách được sắp xếp hoàn chỉnh.
Ưu điểm:
- Hiệu suất ổn định, độ phức tạp thời gian luôn là O(n log n).
Nhược điểm:
- Sử dụng thêm bộ nhớ để lưu trữ các danh sách con.
6. Sắp Xếp Vun Đống (Heap Sort)
Heap Sort sử dụng cấu trúc dữ liệu "heap" để sắp xếp danh sách. Nó xây dựng một heap từ danh sách, sau đó liên tục trích xuất phần tử lớn nhất (hoặc nhỏ nhất) từ heap và đưa nó vào danh sách đã sắp xếp.
Ưu điểm:
- Hiệu suất tốt trong trường hợp xấu nhất, độ phức tạp thời gian luôn là O(n log n).
Nhược điểm:
- Khó cài đặt hơn so với Quick Sort và Merge Sort.
7. Sắp Xếp Đếm (Counting Sort)
Counting Sort là thuật toán sắp xếp không so sánh, hoạt động bằng cách đếm số lần xuất hiện của mỗi phần tử trong danh sách. Nó phù hợp với trường hợp danh sách có phạm vi giá trị nhỏ.
Ưu điểm:
- Hiệu suất rất nhanh, độ phức tạp thời gian là O(n + k), với k là phạm vi giá trị.
Nhược điểm:
- Không phù hợp với danh sách có phạm vi giá trị lớn.
Lời Kết
Việc lựa chọn thuật toán sắp xếp phù hợp phụ thuộc vào đặc thù của dữ liệu và yêu cầu của ứng dụng. Hiểu rõ ưu nhược điểm của từng thuật toán sẽ giúp bạn đưa ra lựa chọn tối ưu, từ đó tối ưu hóa hiệu suất chương trình của mình.













