Tổng hợp tất cả các kiến thức về hàm số bậc nhất và dạng bài tập thường gặp

Để đạt được thành công trong việc giải các bài toán liên quan đến hàm số bậc nhất, chúng ta cần nắm vững định nghĩa và các công thức tính liên quan. Dưới đây, chúng ta sẽ tìm hiểu về hàm số bậc nhất và các dạng bài tập thường gặp để có thể nắm vững kiến thức này.

1. Hàm số bậc nhất là gì?

Hàm số bậc nhất là hàm số được biểu diễn bởi công thức y = ax + b, trong đó a và b là các số đã cho và a ≠ 0. Khi b = 0, hàm số bậc nhất có dạng y = ax, biểu thị một tương quan tỉ lệ thuận giữa y và x.

Tính chất cần nhớ:

• Hàm số bậc nhất y = ax + b xác định với mọi giá trị của x thuộc R và có các tính chất sau:
  • Đồng biến trên R nếu a > 0.
  • Nghịch biến trên R nếu a < 0.

1.1 Lý thuyết hàm số bậc nhất

Hàm số bậc nhất là gì? Đó chính là câu hỏi mà Monkey sẽ giải đáp ngay bây giờ. Hàm số bậc nhất là hàm số được biểu diễn bởi công thức y = ax + b, với a và b là các số đã cho và a ≠ 0. Khi b = 0, hàm số bậc nhất có dạng y = ax, biểu thị một tương quan tỉ lệ thuận giữa y và x.

Các tính chất cần ghi nhớ:

• Hàm số bậc nhất y = ax + b được xác định với mọi giá trị của x thuộc R và có các tính chất sau:
  • Đồng biến trên R nếu a > 0
  • Nghịch biến trên R nếu a < 0

1.2 Các dạng bài tập cơ bản thường gặp

Bài tập về hàm bậc nhất có 2 dạng cụ thể như sau:

Dạng 1: Xác định hàm số bậc nhất

Hàm số bậc nhất là hàm số có dạng y = ax + b (a≠0).

Ví dụ: Với điều kiện nào của m thì các hàm số nào sau đây là hàm số bậc nhất? a) y = (m-1)x + m b) y = (m2-2x -3)x2 + (m+1)x + m c) y = √(m2-1).x + 2

Hướng dẫn giải: a) y = (m-1)x + m là hàm số bậc nhất y = (m-1)x + m ⇔ m - 1 ≠ 0 ⇔ m ≠ 1. Vậy với mọi m ≠ 1 thì hàm số y = (m - 1)x + m là hàm số bậc nhất.

b) y = (m2-2x -3)x2 + (m+1)x + m là hàm số bậc nhất y = (m2-2x -3)x2 + (m+1)x + m ⇔ m - 3 = 0 ⇔ m = 3 Vậy với m = 3 thì hàm số y = (m2-2x -3)x2 + (m+1)x + m là hàm số bậc nhất.

c) y = √(m2-1).x + 2 là hàm số bậc nhất ⇔ √(m2-1) ≠ 0 ⇔ m2 - 1 > 0 ⇔ m > 1 hoặc m < -1. Vậy với m > 1 hoặc m < -1 thì hàm số y = √(m2-1).x + 2 là hàm số bậc nhất.

Dạng 2: Tìm m để hàm số đồng biến, nghịch biến

Ta có hàm số bậc nhất y = ax + b, (a≠0)

• Đồng biến trên R nếu a > 0
• Nghịch biến trên R nếu a < 0

Ví dụ: Tìm a để các hàm số dưới đây : a) y = (a + 2)x + 3 đồng biến trên R. b) y = (m2 - m).x + m nghịch biến trên R.

Hướng dẫn giải: a) y = (a + 2)x + 3 đồng biến trên R y = (a + 2)x + 3 ⇔ a + 2 > 0 ⇔ a > -2. Vậy với mọi a > -2 thì hàm số y = (a + 2)x + 3 đồng biến trên R.

b) y = (m2 - m).x + m nghịch biến trên R y = (m2 - m).x + m ⇔ m2 - m < 0 ⇔ m(m - 1) < 0 ⇔ 0 < m < 1. Vậy với 0 < m < 1 thì hàm số y = (m2 - m).x + m nghịch biến trên R.

2. Đồ thị hàm số bậc nhất

Sau khi đã nắm vững khái niệm về hàm số bậc nhất, chúng ta cần phải hiểu rõ về đồ thị của hàm số bậc nhất. Điều này giúp chúng ta có thể giải được các bài toán liên quan đến đồ thị hàm số bậc nhất.

2.1 Lý thuyết hàm số bậc nhất và đồ thị

Đồ thị của hàm số y = ax + b, (a≠0) là một đường thẳng cắt trục tung tại điểm có tung độ bằng b, song song với đường thẳng y = ax nếu b ≠ 0 và trùng với đường thẳng y = ax nếu b = 0.

Lưu ý rằng đồ thị của hàm số bậc nhất y = ax + b, (a≠0) còn được gọi là đường thẳng y = ax + b, với b được gọi là tung độ gốc của đường thẳng.

2.2 Cách vẽ đồ thị hàm số bậc nhất

Trường hợp 1:

Khi b = 0 thì y = ax là đường thẳng đi qua gốc tọa độ O(0;0) và điểm A (1;a) đã biết.

Trường hợp 2: Xét y = ax với a khác 0 và b khác 0.

Ta đã biết đồ thị hàm số y = ax + b là một đường thẳng, do đó về nguyên tắc ta chỉ cần xác định được hai điểm phân biệt nào đó của đồ thị rồi vẽ đường thẳng qua hai điểm đó.

• Cách thứ nhất:

  • Xác định hai điểm bất kỳ của đồ thị, chẳng hạn:
    • Cho x = 1 tính được y = a + b, ta có điểm A (1; a+b)
    • Cho x = -1 tính được y = -a + b, ta có điểm B (-1 ; -a + b)

• Cách thứ hai:

  • Xác định giao điểm của đồ thị với hai trục tọa độ:
    • Cho x = 0 tính được y = b, ta được điểm C (-b/a;0)
    • Cho y = 0 tính được x = -b/a, ta có điểm D (-b/a; 0)
  • Vẽ đường thẳng qua A, B hoặc C, D ta được đồ thị của hàm số y = ax + b

Trường hợp 3: Khi b khác 0

Ta cần xác định hai điểm phân biệt bất kì thuộc đồ thị.

Bước 1: Cho x = 0 ⇒ y = b. Ta được điểm P(0;b)∈Oy.

Cho y = 0 ⇒ x = −b/a. Ta có điểm Q(−b/a;0)∈Ox.

Bước 2: Vẽ đường thẳng đi qua hai điểm P và Q, ta được đồ thị của hàm số y = ax + b.

2.3 Bài tập vẽ đồ thị hàm số thường gặp có lời giải

Bài tập 1: Vẽ đồ thị hàm số y = x + 2

Hướng dẫn giải: Ta có: x = 0 ⇒ y = 2 x = −1 ⇒ y = 1 → Đồ thị hàm số y = x + 2 đi qua 2 điểm (0;2) và (−1;1).

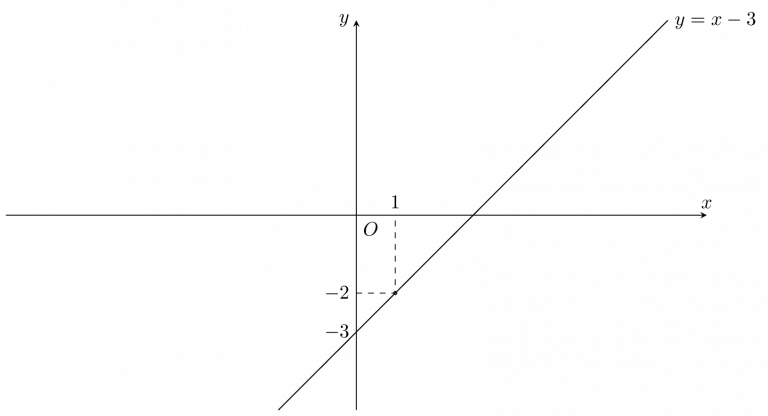
Bài tập 2: Vẽ đồ thị hàm số y = x − 3

Hướng dẫn giải: Ta có: x = 0 ⇒ y = −3 x= 3 ⇒ y = 0 → Đồ thị hàm số y = x − 3 đi qua 2 điểm (0;−3) và (3;0).

3. Sự biến thiên của hàm số bậc nhất

Một kiến thức quan trọng khác mà chúng ta cần quan tâm khi học bài toán này đó chính là sự biến thiên của hàm số bậc nhất. Lý thuyết và cách giải bài tập về sự biến thiên của hàm số bậc nhất cụ thể như sau:

3.1 Hàm số bậc nhất đồng biến và nghịch biến

Định nghĩa hàm số bậc nhất đồng biến khi nào? Và nghịch biến khi nào? Thường rất dễ bị nhầm lẫn trong quá trình ghi nhớ của các bạn học sinh. Nhất là những bạn học sinh cuối cấp và có rất nhiều công thức để ghi nhớ. Vậy, hãy cùng Monkey ôn lại định nghĩa về sự biến thiên của hàm số bậc nhất sau đây nhé!

Hàm số bậc nhất y = ax + b, (a≠0) có tập xác định D = R, đồng biến trên R nếu a > 0 và nghịch biến trên R nếu a < 0.

Bảng biến thiên của hàm số bậc nhất: | a | y = ax + b | |-----------|------------| | a > 0 | Tăng | | a < 0 | Giảm |

3.2 Các dạng bài tập về sự biến thiên của hàm số bậc nhất

Bài tập 1: Tìm k để các hàm số sau a) y = 5x - (2-x)k đồng biến, nghịch biến. b) y = (k2 - 4)x - 2 đồng biến. c) y = (-k2 + k - 1)x - 7 nghịch biến. d) y = (4 - 4k + k2)x + 2 đồng biến.

Hướng dẫn giải: a) y = 5x - (2-x)k = 5x - 2k + k.x = (5+k)x - 2k Vậy hàm số có hệ số a = 5+k. Khi đó:

• Hàm số đồng biến a > 0 ⇔ 5 + k > 0 ⇔ k > -5
• Hàm số nghịch biến a < 0 ⇔ 5 + k < 0 ⇔ k < -5

b) y = (k2 - 4)x - 2 đồng biến khi a > 0 y = (k2 - 4)x - 2 Vậy hàm số đồng biến khi a > 0 ⇔ (k2 - 4) > 0 ⇔ (k+2)(k-2) > 0 ⇔ -2 < k < 2

c) y = (-k2 + k - 1)x - 7 nghịch biến khi a < 0 y = (-k2 + k - 1)x - 7 Vậy hàm số nghịch biến khi a < 0 ⇔ (-k2 + k - 1) < 0 ⇔ k^2 - k + 1 > 0

d) y = (4 - 4k + k2)x + 2 đồng biến khi a > 0 y = (4 - 4k + k2)x + 2 Vậy hàm số đồng biến khi a > 0 ⇔ (4 - 4k + k2) > 0 ⇔ (k-2)(k-2) > 0 ⇔ k = 2

Trên đây là tất cả kiến thức về hàm số bậc nhất mà Monkey đã tổng hợp giúp bạn. Hy vọng với những chia sẻ thực tế này, sẽ giúp bạn có một hành trang vững vàng hơn trong kì thi sắp tới. Xin được đồng hành cùng bạn!

Ba mẹ muốn con học giỏi môn Toán, đồng thời cải thiện khả năng ngôn ngữ tốt hơn thì đừng bỏ qua ứng dụng Monkey Math nhé!

Xem thêm:

• Gợi ý đề toán lớp 1 nâng cao có hướng dẫn giải giúp con đạt kết quả tốt
• Tổng hợp kiến thức cơ bản về tính chất giao hoán trong toán học
• Hình tam giác là gì? Tất tần tật kiến thức chi tiết đầy đủ nhất