Bài viết này sẽ giới thiệu với bạn giải thuật Sàng Eratos và cách thực hiện nó hiệu quả. Sàng Eratos là một giải thuật tìm số nguyên tố trên đoạn $[1;n]$ với độ phức tạp $O(n log log n)$.
Ý tưởng giải thuật
Giải thuật hoạt động như sau:
- Tạo một sàng các số từ $1$ tới $n$ và đánh dấu $1$ không phải là số nguyên tố.
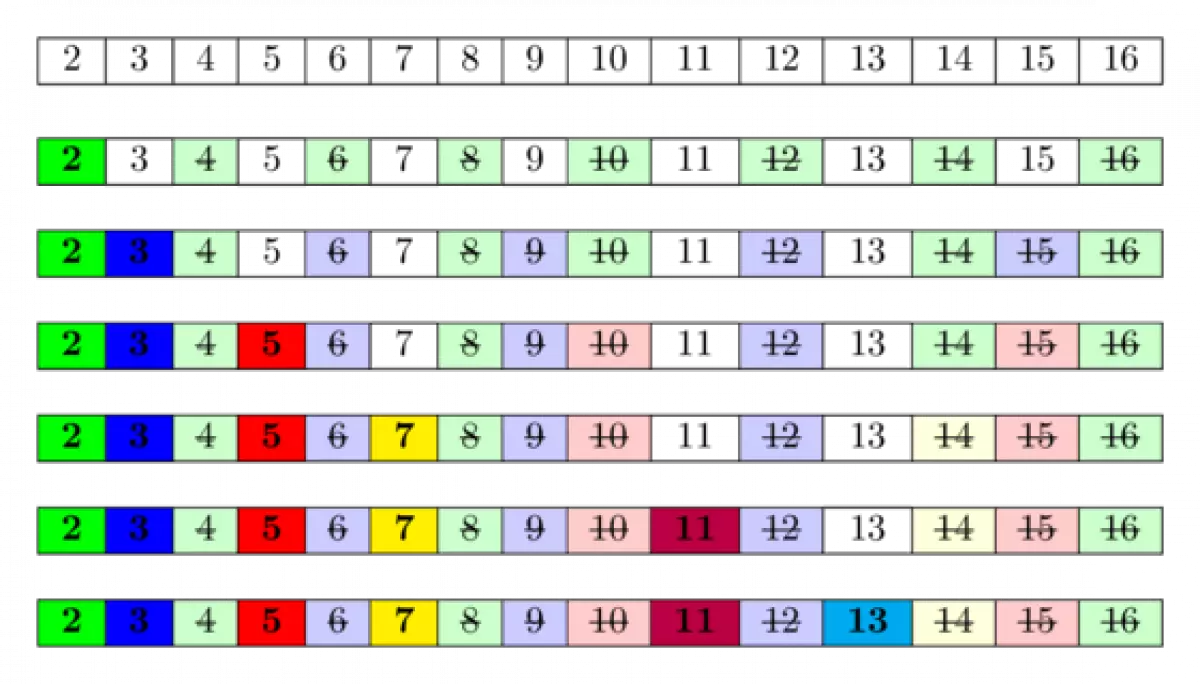
- Bắt đầu từ số nguyên tố đầu tiên là $2$, đánh dấu tất cả các bội số của $2$ là hợp số (ví dụ: $4, 6, 8, ...$).
- Tiếp tục duyệt tới số nguyên tố tiếp theo (chưa bị đánh dấu là hợp số), tìm được $3$. Tại $3$, đánh dấu tất cả các bội số của $3$ là hợp số (ví dụ: $6, 9, 12, ...$).
- Lặp lại quá trình trên để tìm được các số nguyên tố tiếp theo (ví dụ: số nguyên tố tiếp theo sau $3$ là $5$).
Cải tiến giải thuật
Tuy giải thuật trên có độ phức tạp tốt, nhưng cần duyệt qua mọi số trong đoạn $[1, n]$, có thể tốn nhiều thời gian và không gian lưu trữ nếu $n$ lớn. Dưới đây là một số cải tiến giải thuật:
Duyệt đến $sqrt{n}$
Để tìm tất cả số nguyên tố trong đoạn $[1, n]$, ta chỉ cần duyệt đến $\sqrt{n}$. Cải tiến này không giảm độ phức tạp của giải thuật, nhưng giúp giảm số thao tác.
Bỏ qua số chẵn
Vì bội số của $2$ đã được đánh dấu là hợp số từ bước đầu tiên, ta có thể bỏ qua việc đánh dấu các bội số của $2$ trong các bước tiếp theo. Cải tiến này giúp giảm nửa vùng nhớ cần thiết và số thao tác.
Giảm không gian lưu trữ
Để tiết kiệm không gian lưu trữ, giải thuật này chỉ cần dùng $n$ bit trong bộ nhớ (với kiểu dữ liệu boolean) thay vì $n$ byte. Phương pháp này được gọi là "bit-level compression". Tuy nhiên, việc đọc/ghi trên bit có thể làm chậm thuật toán, nên chỉ nên áp dụng khi $n$ là quá lớn và không thể cấp đủ vùng nhớ tương ứng.
Phân đoạn sàng
Trong cải tiến duyệt đến $\sqrt{n}$ ở trên, ta không cần duy trì thông tin về tất cả các số nguyên tố trong đoạn $[1, \sqrt{n}]$ tại mọi thời điểm. Thay vào đó, ta chỉ cần lưu trữ các số nguyên tố trong đoạn này để thực hiện sàng. Sau đó, ta sẽ tách đoạn thành các phân đoạn nhỏ hơn để xét tương ứng, dựa trên các số nguyên tố đã được sàng trước đó. Cải tiến này giúp giảm số lượng thao tác cần thiết để tìm tất cả số nguyên tố trong đoạn $[1, n]$.
Ví dụ với đoạn $[L, R]$
Nếu bạn cần tìm tất cả các số nguyên tố trong đoạn $[L, R]$ với $R - L + 1 \approx 10^7$ và $R$ có thể rất lớn (ví dụ: $R = 10^{12}$), ta có thể sử dụng phương pháp phân đoạn sàng như đã trình bày ở trên và tính trước các số nguyên tố trong đoạn $[1, \sqrt{R}]$. Độ phức tạp của giải thuật tùy thuộc vào cách thực hiện, nhưng có thể được giảm xuống $O((R - L + 1) log log (R) + \sqrt{R} log log \sqrt{R})$.
Giải thuật theo thời gian tuyến tính
Bài viết cũng đề cập đến việc thay đổi giải thuật sàng để có độ phức tạp thời gian tuyến tính. Tuy nhiên, mỗi giải thuật đều có nhược điểm riêng. Chi tiết giải thuật này được trình bày trong bài viết "Sieve of Eratosthenes Having Linear Time Complexity".
Bài tập thực hành
Sau đây là một số bài tập liên quan để bạn ôn tập và áp dụng giải thuật sàng Eratos:
- SPOJ - Printing Some Primes
- SPOJ - A Conjecture of Paul Erdos
- SPOJ - Primal Fear
- SPOJ - Primes Triangle (I)
- Codeforces - Almost Prime
- Codeforces - Sherlock And His Girlfriend
- SPOJ - Namit in Trouble
- SPOJ - Bazinga!
- Project Euler - Prime pair connection
- SPOJ - N-Factorful
- SPOJ - Binary Sequence of Prime Numbers
- UVA 11353 - A Different Kind of Sorting
- SPOJ - Prime Generator
- SPOJ - Printing some primes (hard)
- Codeforces - Nodbach Problem
- Codeforces - Colliders
Chúc bạn thành công trong việc nắm vững giải thuật Sàng Eratos và áp dụng nó để giải quyết các bài toán liên quan đến số nguyên tố!












