Chương 14: Hashing- 1.Lý thuyết cơ bản

Hashing là một kỹ thuật được sử dụng để lưu trữ và truy xuất thông tin càng nhanh càng tốt. Nó được sử dụng để thực hiện các tìm kiếm tối ưu và rất hữu ích trong việc triển khai các symbol tables.

Trong chương Trees, chúng ta đã thấy rằng cây tìm kiếm nhị phân cân bằng hỗ trợ các thao tác như chèn, xóa và tìm kiếm trong thời gian O(logn). Trong các ứng dụng, nếu chúng ta cần các thao tác này trong O(1), thì hashing cung cấp một cách. Hãy nhớ rằng độ phức tạp trong trường hợp xấu nhất của hàm băm vẫn là O(n), nhưng nó cho kết quả trung bình là O(1).

Các operations phổ biến trong một Hash table là:

• CreatHashTable: Tạo bảng băm mới
• HashSearch: Tìm kiếm khóa trong bảng băm
• Hashlnsert: Chèn khóa mới vào bảng băm
• HashDelete: Xóa khóa khỏi bảng băm
• DeleteHashTable: Xóa bảng băm

Nói một cách đơn giản, chúng ta có thể coi array là một hash table. Để hiểu việc sử dụng bảng băm, chúng ta hãy xem xét ví dụ sau: Đưa ra thuật toán in ký tự lặp lại đầu tiên nếu có các phần tử trùng lặp trong đó. Hãy để chúng ta suy nghĩ về các giải pháp có thể. Cách giải quyết đơn giản và mạnh mẽ là: với chuỗi đã cho, với mỗi ký tự kiểm tra xem ký tự đó có lặp lại hay không. Time complexity của phương pháp này là O(n2) với space complexity O(1).

Bây giờ, chúng ta hãy tìm một giải pháp tốt hơn cho vấn đề này. Vì mục tiêu của chúng ta là tìm ký tự lặp lại đầu tiên, nếu chúng ta nhớ các ký tự trước đó trong một mảng nào đó thì sao?

chúng ta biết rằng số ký tự có thể có là 256 (để đơn giản, chỉ giả sử các ký tự ASCII). Đối với mỗi ký tự đầu vào, hãy chuyển đến vị trí tương ứng và tăng số lượng của nó. Vì chúng ta đang sử dụng mảng, nên phải mất constant time để đến bất kỳ vị trí nào. Trong khi quét đầu vào, nếu chúng ta nhận được một ký tự có bộ đếm đã là 1 thì chúng ta có thể nói rằng ký tự đó là ký tự lặp lại lần đầu tiên.

public void findFirstRepeatedChar(char[] str){
    int count[] = new int[256];
    for (int i = 0; i < 256; i++) {
        count[i] = 0;
    }
    for (int i = 0; i < str.length; i++) {
        if (count[str[i]] == 1){
            System.out.println(str[i]);
            return;
        } else {
            count[str[i]]++;
        }
    }
    System.out.println("No repeated characters");
}

Tại sao không phải Array?

Trong bài toán trước, chúng ta đã sử dụng một mảng có kích thước 256 vì chúng ta biết trước số ký tự có thể khác nhau [256]. Bây giờ, chúng ta hãy xem xét một biến thể nhỏ của cùng vấn đề này. Giả sử mảng đã cho có số thay vì ký tự thì ta giải bài toán như thế nào?

Trong trường hợp này, tập hợp các giá trị có thể là vô cùng (hoặc ít nhất là rất lớn). Không thể tạo một mảng lớn và lưu trữ các bộ đếm. Điều đó có nghĩa là có một số lượng key vô cùng nhiều và chúng ta có giới hạn trong bộ nhớ. Nếu chúng ta muốn giải quyết vấn đề này, chúng ta cần bằng cách nào đó ánh xạ tất cả các keys có thể này tới các vị trí bộ nhớ có thể. Từ những gì đã thảo luận và sơ đồ ở trên, có thể thấy rằng chúng ta cần ánh xạ các keys có thể đến một trong các vị trí có sẵn. Kết quả là sử dụng các mảng đơn giản không phải là lựa chọn chính xác để giải quyết các vấn đề trong đó các keys có thể rất lớn. Quá trình ánh xạ các keys tới các vị trí được gọi là hashing.

Note: Hiện tại, chúng ta chưa cần quan tâm về cách các keys được ánh xạ tới các vị trí. Điều đó phụ thuộc vào function được sử dụng để thực hiện chuyển đổi. Một chức năng đơn giản như vậy là key % table size.

Hashing có bốn thành phần chính:

1. Hash Table
2. Hash Functions
3. Collisions (Xung đột - xảy ra khi các giá trị giống nhau được tạo ra từ các dữ liệu nguồn khác nhau)
4. Collision Resolution Techniques (Kỹ thuật giải quyết xung đột)

Hash table là một tổng quát của mảng. Với mảng, ta lưu phần tử có key là k tại vị trí k của mảng. Điều đó có nghĩa là, cho trước một khóa k, chúng ta tìm thấy phần tử có khóa k bằng cách chỉ tìm ở vị trí thứ k của mảng. Điều này được gọi là direct addressing (địa chỉ trực tiếp).

Direct addressing được áp dụng khi chúng ta có đủ khả năng phân bổ một mảng với một vị trí cho mọi key có thể. Nhưng nếu chúng ta không có đủ không gian để phân bổ vị trí cho từng key có thể, thì chúng ta cần một cơ chế để xử lý trường hợp này. Một cách khác để xác định kịch bản là: nếu chúng ta có ít vị trí hơn và nhiều key khả thi hơn, thì việc triển khai mảng đơn giản là không đủ.

Trong những trường hợp này, một tùy chọn là sử dụng hash tables. Hash table hoặc Hash map là một cấu trúc dữ liệu lưu trữ các key và giá trị được liên kết của chúng và hash table sử dụng hash function để ánh xạ các khóa tới các giá trị được liên kết của chúng. Quy ước chung là chúng ta sử dụng bảng băm khi số lượng key thực sự được lưu trữ là nhỏ so với số lượng key có thể tồn tại.

Hash Function được sử dụng để chuyển đổi key thành index. Lý tưởng nhất là hash function nên ánh xạ từng khóa có thể tới một vị trí index duy nhất, nhưng rất khó để đạt được điều này trong thực tế.

Với một tập hợp các phần tử, hash function ánh xạ từng mục vào một vị trí duy nhất được gọi là perfect hash function (hàm băm hoàn hảo). Nếu chúng ta biết các phần tử và tập hợp sẽ không bao giờ thay đổi, thì có thể xây dựng một hàm băm hoàn hảo. Thật không may, với một tập hợp các phần tử tùy ý, không có cách nào có hệ thống để xây dựng một hàm băm hoàn hảo. May mắn thay, chúng ta không cần hàm băm phải hoàn hảo để vẫn đạt được performance hiệu quả.

Một cách để luôn có một hàm băm hoàn hảo là tăng kích thước của hash table để mỗi giá trị có thể có trong phạm vi phần tử có thể được cung cấp. Điều này đảm bảo rằng mỗi phần tử sẽ có một vị trí duy nhất. Mặc dù điều này là thực tế đối với số lượng phần tử nhỏ, nhưng nó không khả thi khi số lượng phần tử có thể rất lớn. Ví dụ: nếu các phần tử là số An sinh xã hội gồm chín chữ số, thì phương pháp này sẽ yêu cầu gần một tỷ vị trí. Nếu chúng ta chỉ muốn lưu trữ dữ liệu cho một lớp 25 học sinh, chúng ta sẽ lãng phí một lượng lớn bộ nhớ.

Mục tiêu của chúng ta là tạo ra một hàm băm giảm thiểu số lần collisions (xung đột), dễ tính toán và phân bổ đồng đều các phần tử trong bảng băm.

Phương pháp folding (gấp) để xây dựng các hàm băm bắt đầu bằng cách chia các phần tử thành các phần có kích thước bằng nhau (phần cuối cùng có thể không có kích thước bằng nhau). Những phần này sau đó được cộng lại với nhau để tạo ra giá trị băm thu được. Ví dụ: nếu phần tử của chúng ta là số điện thoại 436-555-4601, chúng ta sẽ lấy các chữ số và chia chúng thành các nhóm 2 (43,65,55,46,01). Sau khi cộng 43+65+55+46+01, ta được 210. Nếu chúng ta giả sử bảng băm của chúng ta có 11 vị trí, thì chúng ta cần thực hiện thêm bước chia cho 11 và giữ phần còn lại. Trong trường hợp này 210 % 11 là 1, vì vậy số điện thoại 436-555-4601 được băm vào vị trí 1. Một số phương pháp folding tiến thêm một bước và đảo ngược mọi nhóm khác trước khi cộng. Đối với ví dụ trên, chúng ta nhận được 43+56+55+64+01=219 mang lại 219 % 11 = 10.

Cách chọn Hash Function?

Các vấn đề cơ bản liên quan đến việc tạo các hash tables là:

• Một hàm băm hiệu quả phải được thiết kế sao cho nó phân phối đồng đều các giá trị index của các đối tượng được chèn trên bảng.
• Một thuật toán giải quyết xung đột hiệu quả nên được thiết kế sao cho nó tính toán index thay thế cho khóa có hash index tương ứng với vị trí đã chèn trước đó trong bảng băm.
• Chúng ta phải chọn một hàm băm có thể được tính toán nhanh chóng, trả về các giá trị trong phạm vi vị trí trong bảng của chúng ta và giảm thiểu collisions.

Đặc điểm của Hash Function tốt

Một hàm băm tốt nên có các đặc điểm sau:

• Giảm thiểu collisions
• Dễ dàng và nhanh chóng để tính toán
• Phân phối các giá trị khóa đồng đều trong bảng băm
• Sử dụng tất cả thông tin được cung cấp trong key
• Có high load factor (hệ số tải) cao cho một bộ khóa nhất định

Hệ số tải của bảng băm không trống là số phần tử được lưu trữ trong bảng chia cho kích thước của bảng. Đây là tham số quyết định được sử dụng khi chúng ta muốn băm lại hoặc mở rộng các mục trong bảng băm hiện có. Điều đó có nghĩa là, nó cho biết hàm băm có phân phối các khóa một cách đồng đều hay không.

Các hàm băm được sử dụng để ánh xạ từng key tới một không gian địa chỉ khác nhau, nhưng thực tế không thể tạo một hàm băm như vậy và vấn đề được gọi là collision (xung đột). Xung đột là tình trạng hai bản ghi được lưu trữ ở cùng một vị trí.

Quá trình tìm kiếm một vị trí thay thế được gọi là collision resolution (giải quyết xung đột). Mặc dù các bảng băm có vấn đề xung đột, nhưng trong nhiều trường hợp, chúng hiệu quả hơn so với tất cả các cấu trúc dữ liệu khác, chẳng hạn như cây tìm kiếm. Có một số kỹ thuật giải quyết xung đột và phổ biến nhất là direct chaining (tạo chuỗi trực tiếp) và open addressing (địa chỉ mở).

• Direct Chaining: Một mảng của Linked List
  • Separate chaining (chuỗi riêng biệt)
• Open Addressing: Triển khai dựa trên mảng
  • Linear probing (linear search) - Thăm dò tuyến tính (tìm kiếm tuyến tính)
  • Quadratic probing (nonlinear search) - Thăm dò bậc hai (tìm kiếm phi tuyến tính)
  • Double hashing (Băm kép - sử dụng hai hàm băm)

Giải quyết xung đột bằng cách xâu chuỗi kết hợp biểu diễn được liên kết với bảng băm. Khi hai hoặc nhiều bản ghi băm vào cùng một vị trí, những bản ghi này được tạo thành một danh sách liên kết được gọi là chain (chuỗi).

Trong Open Addressing, tất cả các khóa được lưu trữ trong chính bảng băm. Cách tiếp cận này còn được gọi là closed hashing. Thủ tục này dựa trên probing (thăm dò). Một xung đột được giải quyết bằng cách thăm dò.

Linear Probing

Khoảng thời gian giữa các probes (đầu dò) được cố định ở mức 1. Trong thăm dò tuyến tính, chúng ta tìm kiếm bảng băm một cách tuần tự, bắt đầu từ vị trí băm ban đầu. Nếu một vị trí đã bị chiếm, chúng ta sẽ kiểm tra vị trí tiếp theo. chúng ta có thể tìm từ vị trí cuối cùng của hash table đến vị trí đầu tiên nếu cần thiết. Hàm để rehashing (băm lại) như sau:

Một trong những vấn đề với thăm dò tuyến tính là các phần tử trong bảng có xu hướng nhóm lại với nhau trong bảng băm. Điều này có nghĩa là bảng chứa các nhóm vị trí đã bị chiếm liên tiếp được gọi là clustering (phân cụm).

Các cụm có thể đến gần nhau và hợp nhất thành một cụm lớn hơn. Do đó, một phần của bảng có thể khá dày đặc, mặc dù phần khác có tương đối ít các phần tử. Phân cụm gây ra các tìm kiếm thăm dò dài và do đó làm giảm hiệu quả tổng thể.

Vị trí tiếp theo được thăm dò được xác định bởi kích thước bước, trong đó có thể có các kích thước bước khác (nhiều hơn một).

Quadratic Probing

Khoảng thời gian giữa các probes (đầu dò) tăng tỷ lệ thuận với giá trị băm (khoảng thời gian do đó tăng tuyến tính và các chỉ số được mô tả bằng hàm bậc hai). Vấn đề Clustering (phân cụm) có thể được loại bỏ nếu chúng ta sử dụng phương pháp thăm dò bậc hai.

Trong thăm dò bậc hai, chúng ta bắt đầu từ vị trí băm ban đầu i. Nếu một vị trí có người sử dụng, chúng ta kiểm tra các vị trí i+1^2, i+2^2, i+3^2, i+4^2,... chúng ta có thể tìm từ vị trí cuối cùng của hash table đến vị trí đầu tiên nếu cần thiết. Hàm để rehashing (băm lại) như sau:

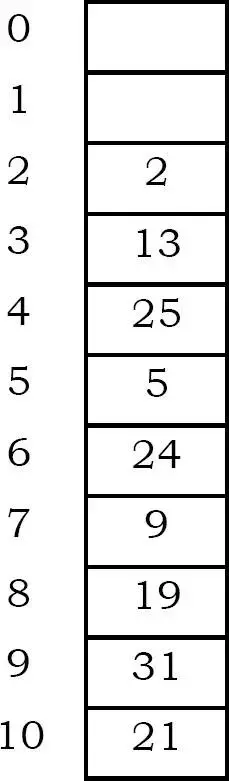
Ví dụ: Giả sử rằng kích thước bảng là 11 (0..10)

Hash Function: h(key) = key mod 11 Thêm key:

• 31 mod 11 = 9
• 19 mod 11 = 8
• 2 mod 11 = 2
• 13 mod 11 = 2 → 2 + 12 = 3
• 25 mod 11 = 3 → 3 + 12=4
• 24 mod 11 = 2 → 2 + 12, 2 + 22 = 6
• 21 mod 11 = 10
• 9 mod 11 = 9 → 9 + 121^212, 9 + 222^222 mod 11, 9 + 323^232 mod 11=7

Mặc dù việc phân cụm tránh được bằng thăm dò bậc hai, nhưng vẫn có cơ hội phân cụm. Phân cụm được gây ra bởi nhiều keys được ánh xạ tới cùng một hash key. Do đó, trình tự thăm dò cho các keys như vậy bị kéo dài bởi các xung đột lặp đi lặp lại dọc theo trình tự thăm dò. Cả thăm dò tuyến tính và bậc hai đều sử dụng trình tự thăm dò độc lập với search key đầu vào.

Double Hashing

Khoảng giữa các đầu dò được tính toán bởi một hàm băm khác. Double hashing (Băm kép) làm giảm phân cụm theo cách tốt hơn. Gia tăng cho trình tự thăm dò được tính toán bằng cách sử dụng hàm băm thứ hai. Hàm băm thứ hai h2 là:

Đầu tiên chúng ta thăm dò vị trí h1(key). Nếu vị trí đã bị chiếm, chúng ta thăm dò vị trí h1(key)+h2(key), h1(key)+2∗h2(key),...h1(key) + h2(key), h1(key) + 2 * h2(key), ...

Example: Giả sử rằng kích thước bảng là 11 (0..10)

• Hash Function: giả sử h1(key) = key mod 11 and h2(key) = 7- (key mod 7)
• Thêm key:
  • 58 mod 11 = 3
  • 14 mod 11 = 3 → 3 + 7 = 10
  • 91 mod 11 = 3 → 3+ 7,3+ 2* 7 mod 11 = 6
  • 25 mod 11 = 3 → 3 + 3,3 + 2*3 = 9

So sánh: Open Addressing vs. Separate Chaining

• Nó hơi phức tạp vì chúng ta phải tính đến việc sử dụng bộ nhớ. Separate chaining sử dụng thêm bộ nhớ cho các linked list. Open addressing cần thêm bộ nhớ ngầm trong bảng để kết thúc trình tự thăm dò. Open-addressed hash tables không thể được sử dụng nếu dữ liệu không có khóa duy nhất.

So sánh: Các phương thức của Open Addressing

• Linear Probing
  • Nhanh nhất trong 3 phương thức
  • Dễ nhất để implement và deploy
  • Sử dụng bộ nhớ hiệu quả hơn
  • Sử dụng ít probers(đầu dò)
  • Sử dụng nhiều bộ nhớ bổ sung cho links và nó không thăm dò toàn bộ các vị trí trong bảng
• Quadratic Probing
  • Sử dụng ít probers(đầu dò) nhưng tốn thời gian hơn
  • Một vấn đề xảy ra được gọi là primary clustering(phân cụm chính)
• Double Hashing
  • Phức tạp hơn để implement
  • Sử dụng ít probers(đầu dò) nhưng tốn thời gian hơn
  • Một vấn đề xảy ra được gọi là secondary clustering(phân cụm thứ cấp)