Tiếp tục với chuyên mục Toán Học, hôm nay chúng ta sẽ cùng tìm hiểu về các công thức đạo hàm trong toán học một cách đầy đủ và chi tiết. Chúng ta sẽ cùng khám phá công thức đạo hàm căn bậc 3, đạo hàm căn bậc 3 của x, đạo hàm căn bậc 3 của x², đạo hàm căn u, đạo hàm bậc 2, đạo hàm căn bậc 2 của x, căn u đạo hàm, công thức đạo hàm log, công thức đạo hàm logarit và đạo hàm căn x. Các công thức này sẽ giúp bạn áp dụng vào làm bài tập một cách dễ dàng.
Định nghĩa đạo hàm
Đạo hàm của một hàm số y = f(x) tại điểm x0 là tỉ số giữa số gia của hàm số và số gia của đối số tại x0, khi số gia của đối số tiến dần tới 0. Nếu hàm số f(x) có đạo hàm tại x0, thì nó liên tục tại điểm đó.
Quy tắc cơ bản của đạo hàm
Quy tắc đạo hàm của hàm số hợp: Nếu y = y(u(x)), thì y'(x) = y'(u) . u'(x).
Công thức đạo hàm từ cơ bản đến nâng cao
1. Công thức đạo hàm cơ bản
2. Công thức đạo hàm lượng giác
3. Bảng đạo hàm
Các dạng bài tập liên quan đến công thức đạo hàm
Dạng 1: Tính đạo hàm bằng định nghĩa
Dạng 2: Tính đạo hàm bằng công thức
Dạng 3: Tính đạo hàm của hàm số lượng giác
Dạng 4: Chứng minh đẳng thức, giải phương trình, bất phương trình liên quan đến đạo hàm
Bài viết này nhằm giúp bạn học tốt hơn với công thức đạo hàm, cũng như là một tài liệu ôn luyện lại các kiến thức đã học một cách đơn giản và đầy đủ nhất về công thức đạo hàm lượng giác, công thức đạo hàm nguyên hàm và các công thức khác. Hãy sẵn sàng để thử áp dụng vào các bài tập và nắm vững kiến thức này nhé!
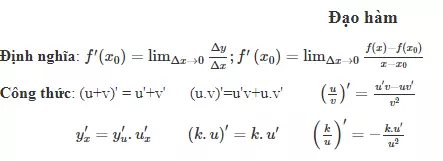Hình ảnh minh họa công thức đạo hàm
Hình ảnh minh họa công thức đạo hàm
Hình ảnh minh họa công thức đạo hàm
Hình ảnh minh họa công thức đạo hàm
Hình ảnh minh họa công thức đạo hàm
Hình ảnh minh họa công thức đạo hàm
Hình ảnh minh họa công thức đạo hàm
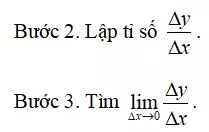Hình ảnh minh họa công thức đạo hàm
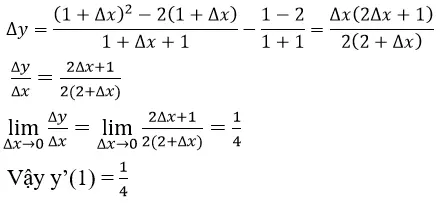Hình ảnh minh họa công thức đạo hàm
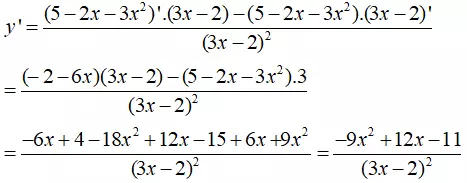Hình ảnh minh họa công thức đạo hàm
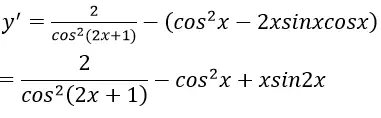Hình ảnh minh họa công thức đạo hàm
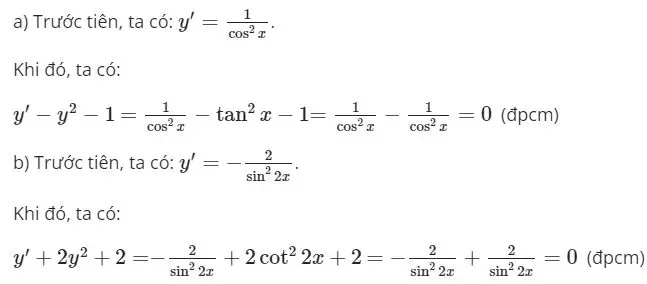Hình ảnh minh họa công thức đạo hàm
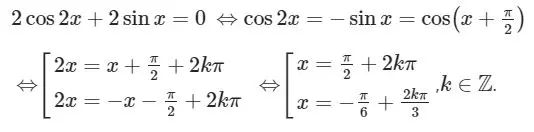Hình ảnh minh họa công thức đạo hàm
Trên đây là những kiến thức cơ bản về công thức đạo hàm mà chúng ta cần nắm vững. Hy vọng rằng bài viết này sẽ giúp các bạn hiểu thêm về công thức đạo hàm và áp dụng thành thạo trong các bài tập. Hãy tiếp tục học tập và rèn luyện, sẽ đến một ngày bạn sẽ trở thành chuyên gia về toán học!
