Bạn có bao giờ gặp khó khăn trong việc giải hệ phương trình chưa? Giờ đây, với trang web trực tuyến của HocTapHay.Com, bạn có thể giải hệ phương trình một cách dễ dàng và chính xác. Bạn có thể sử dụng bảng tính trực tuyến để so sánh kết quả tính toán và đánh giá kết quả học tập của mình.
Khám phá Đồ thị
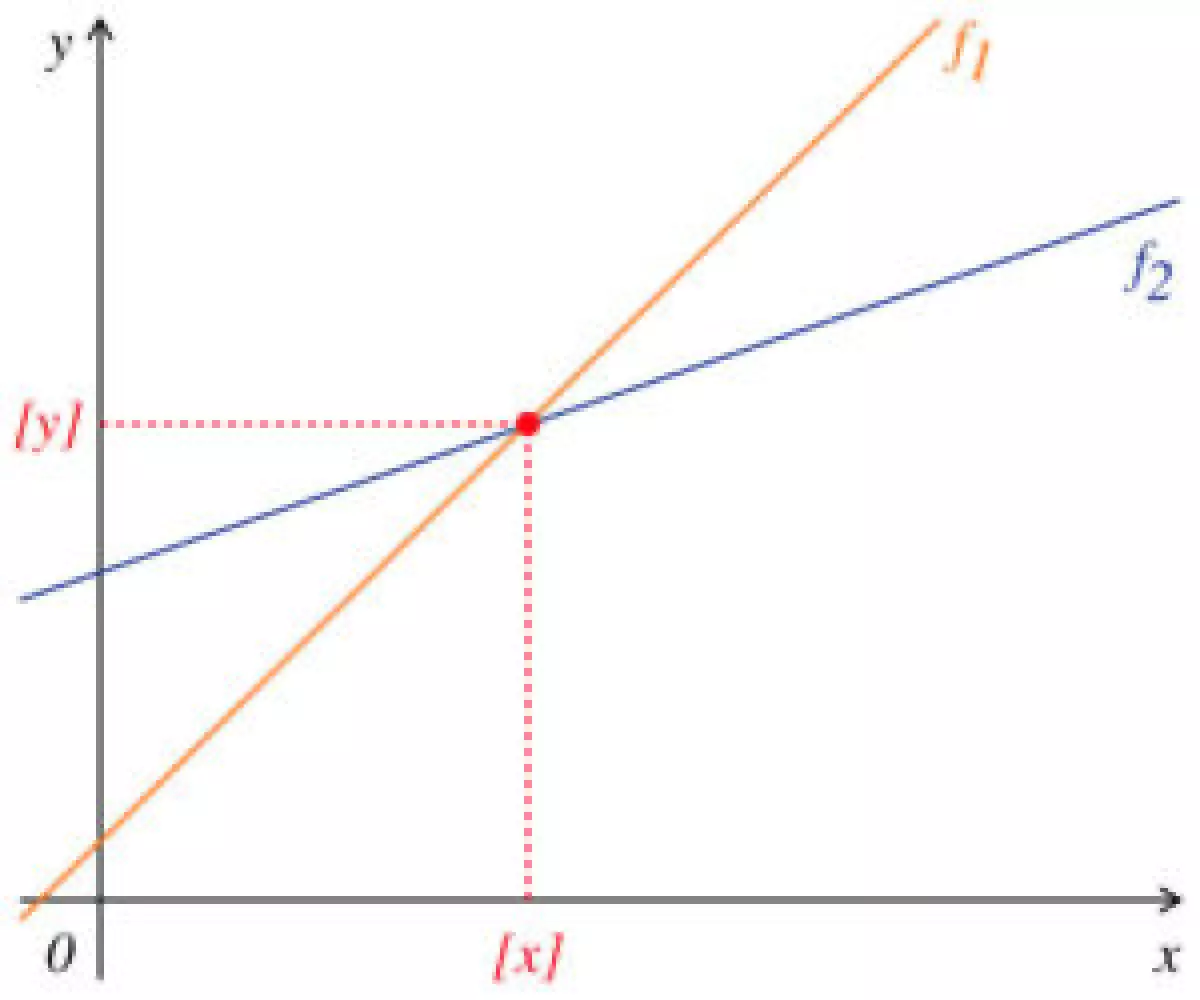Hình ảnh minh họa về Hệ Phương Trình
Trước khi bắt đầu giải hệ phương trình, hãy cùng tìm hiểu về khái niệm cơ bản của nó.
Khái niệm Hệ Phương Trình Bậc Nhất Hai Ẩn Số
Hệ phương trình bậc nhất hai ẩn số là hệ phương trình có dạng:
{ ax + by = c (1)
{ a'x + b'y = c' (2)Trong đó a, b, c, a', b', c' là các số thực đã được cho trước, và x và y là ẩn số.
Nếu hai phương trình (1) và (2) có nghiệm chung là (x₀, y₀), thì (x₀, y₀) được gọi là nghiệm của hệ phương trình. Ngược lại, nếu hai phương trình (1) và (2) không có nghiệm chung, ta nói hệ phương trình vô nghiệm.
Cách giải Hệ Phương Trình Bậc Nhất Hai Ẩn
Dạng 1: Giải hệ phương trình bằng phương pháp thế
Giải hệ phương trình bằng phương pháp thế như sau:
{ 3x - 2y = 4
{ 2x + y = 5Thay y trong phương trình thứ nhất bằng giá trị của nó trong phương trình thứ hai, ta có:
{ 3x - 2(5 - 2x) = 4
{ y = 5 - 2xTiếp tục giải phương trình và tìm giá trị của x và y, ta có:
{ 7x = 14
{ y = 5 - 2xSuy ra:
{ x = 2
{ y = 1Vậy hệ phương trình đã cho có nghiệm duy nhất (x, y) = (2, 1).
Dạng 2: Giải hệ phương trình bằng phương pháp cộng đại số
Giải hệ phương trình bằng phương pháp cộng đại số như sau:
{ 3x - 2y = 4
{ 2x + y = 5Cộng phương trình thứ nhất với phương trình thứ hai, ta có:
{ 3x - 2y = 4
{ 4x + 2y = 10Tiếp tục giải phương trình và tìm giá trị của x và y, ta có:
{ 7x = 14
{ 2x + y = 5Suy ra:
{ x = 2
{ y = 1Vậy hệ phương trình đã cho có nghiệm duy nhất (x, y) = (2, 1).
Dạng 3: Giải hệ phương trình bằng phương pháp đặt ẩn số phụ
Giải hệ phương trình bằng phương pháp đặt ẩn số phụ như sau:
-
{ 1/x + 1/y = 1/12 { 8/x + 15/y = 1 -
{ 2/(x + 2y) + 1/(y + 2x) = 3 { 4/(x + 2y) - 3/(y + 2x) = 1 -
{ 3x/(x + 1) - 2/(y + 4) { 2x/(x + 1) - 5/(y + 4) = 9 -
{ x^2 + y^2 = 13 { 3x^2 - 2y^2 = -6 -
{ 3√x + 2√y = 16 { 2√x - 3√y = -11 -
{ |x| + 4|y| = 18 { 3|x| + |y| = 10
Dạng 4: Giải và biện luận hệ phương trình
Phương pháp giải và biện luận hệ phương trình như sau:
- Từ một phương trình của hệ, tìm y theo x và thay vào phương trình còn lại để có phương trình bậc nhất đối với x.
- Giả sử phương trình bậc nhất đối với x có dạng ax = b.
- Biện luận phương trình ax = b để xác định sự biện luận của hệ.
i) Nếu a = 0, phương trình trở thành 0x = b:
- Nếu b = 0, thì hệ có vô số nghiệm.
- Nếu b ≠ 0, thì hệ vô nghiệm.
ii) Nếu a ≠ 0, ta có phương trình ax = b (⇒ x = b/a).
- Thay vào biểu thức của x để tìm y, lúc đó hệ phương trình có nghiệm duy nhất.
Ví dụ: Giải và biện luận hệ phương trình:
{ mx - y = 2m
{ 4x - my = m + 6Từ phương trình thứ nhất, ta có y = mx - 2m. Thay vào phương trình thứ hai, ta được:
{ (m^2 - 4)x = (2m + 3)(m - 2)i) Nếu m^2 - 4 ≠ 0, tức là m ≠ ±2, thì:
- x = (2m + 3)/(m + 2)
- y = -m/(m + 2)
Hệ có nghiệm duy nhất là ((2m + 3)/(m + 2), -m/(m + 2)).
ii) Nếu m = 2, thì phương trình trở thành:
- x = (2m + 3)/(m + 2) = (2*2 + 3)/(2 + 2) = 5/4
- y = mx - 2m = 2x - 4
Hệ có vô số nghiệm (x, 2x - 4) với mọi x ∈ R.
iii) Nếu m = -2, thì phương trình trở thành 0x = 4. Hệ vô nghiệm.
Vậy:
- Nếu m ≠ ±2, thì hệ có nghiệm duy nhất là ((2m + 3)/(m + 2), -m/(m + 2)).
- Nếu m = 2, thì hệ có vô số nghiệm (x, 2x - 4) với mọi x ∈ R.
- Nếu m = -2, thì hệ vô nghiệm.
Dạng 5: Xác định giá trị của tham số để hệ có nghiệm thỏa mãn điều kiện cho trước
Phương pháp giải như sau:
- Giải hệ phương trình theo tham số.
- Viết x, y của hệ về dạng n + k/f(m) với n, k là số nguyên.
- Tìm m nguyên để f(m) là ước của k.
Ví dụ: Xác định giá trị của m để hệ có nghiệm duy nhất là nghiệm nguyên:
{ mx + 2y = m + 1
{ 2x + my = 2m - 1Như vậy, để hệ phương trình có nghiệm duy nhất là nghiệm nguyên, ta phải tìm giá trị nguyên của m sao cho m + 2 là ước của m + 1.
Chúng ta cùng tìm ra những giá trị của m như thế nào nhé!
Phép Tính Liên Quan
Ngoài việc giải hệ phương trình, HocTapHay.Com còn cung cấp cho bạn nhiều phép tính khác như phương trình bậc hai và phương trình bậc nhất. Hãy khám phá ngay để nâng cao kỹ năng tính toán của bạn!
Hệ Phương Trình Online Phương Trình Bậc Hai Online Phương Trình Bậc Nhất Online
Hy vọng rằng bài viết này đã giúp bạn hiểu rõ hơn về hệ phương trình và cách giải chúng. Hãy truy cập HocTapHay.Com ngay để sử dụng công cụ giải hệ phương trình trực tuyến và tận hưởng quá trình học tập thú vị!
