Công thức Sin 2x

Công thức Sin 2x là một trong những công thức góc kép trong quy tắc lượng giác. Sử dụng công thức này, chúng ta có thể tìm giá trị sin của góc có giá trị gấp đôi. Ta đã quen thuộc với sin là một trong các tỷ số lượng giác chính, được định nghĩa là tỷ số giữa độ dài cạnh đối (của góc) và độ dài cạnh huyền trong tam giác vuông. Có nhiều công thức khác nhau cho sin 2x và có thể xác minh bằng cách sử dụng những công thức lượng giác cơ bản.

Công thức Sin 2x

Công thức sin 2x = 2 sin x cos x

Công thức sin 2x = 2 √(1 - cos^2x) cos x

Công thức sin 2x = 2 sin x √(1 - sin^2x)

Công thức sin 2x = (2 tan x)/(1 + tan^2x)

Trong bài viết này, chúng ta cũng sẽ khám phá khái niệm sin^2x (sin bình phương x) và công thức tương ứng của nó. Chúng ta sẽ biểu diễn công thức sin 2x và sin^2x dưới dạng các khối hàm lượng giác khác nhau bằng cách sử dụng các công thức lượng giác khác nhau và từ đó, suy ra các công thức.

1. Sin 2x là gì?

Sin 2x là một công thức lượng giác trong lượng giác được sử dụng để giải quyết các bài toán lượng giác, tích phân và vi phân phức tạp. Nó được sử dụng để đơn giản hóa các biểu thức lượng giác khác nhau. Công thức sin 2x có thể được biểu diễn dưới dạng khác nhau bằng cách sử dụng các công thức lượng giác khác nhau trong lượng giác. Công thức phổ biến nhất của sin 2x là gấp đôi tích của hàm sin và hàm cos, được biểu diễn toán học bằng công thức sin 2x = 2 sinx cosx. Chúng ta cũng có thể biểu diễn sin 2x chỉ dưới dạng hàm sin/cos/tan.

Miền giá trị của sin 2x là tập hợp tất cả các số thực. Vì miền giá trị của hàm sin là [-1, 1], nên miền giá trị của sin 2x cũng là [-1, 1].

2. Công thức Sin 2x

Công thức sin 2x là công thức góc kép được sử dụng cho hàm sin trong lượng giác. Lượng giác là một nhánh trong toán học nơi chúng ta nghiên cứu mối quan hệ giữa các góc và các cạnh của một tam giác vuông. Có hai công thức cơ bản cho sin 2x:

• Công thức sin 2x = 2 sin x cos x (dưới dạng sin và cos)
• Công thức sin 2x = (2 tan x)/(1 + tan^2x) (dưới dạng tan)

Đây là những công thức chính của sin 2x. Nhưng chúng ta có thể viết công thức này dưới dạng sin x (hoặc) cos x chỉ bằng cách sử dụng công thức đồng nhất lượng giác sin^2x + cos^2x = 1. Sử dụng công thức đồng nhất lượng giác này, chúng ta có thể viết sin x = √(1 - cos^2x) và cosx = √(1 - sin^2x). Do đó, các công thức sin 2x dưới dạng cos và sin là:

• Công thức sin 2x = 2 √(1 - cos^2x) cos x (công thức sin 2x trong dạng cos)
• Công thức sin 2x = 2 sin x √(1 - sin^2x) (công thức sin 2x trong dạng sin)

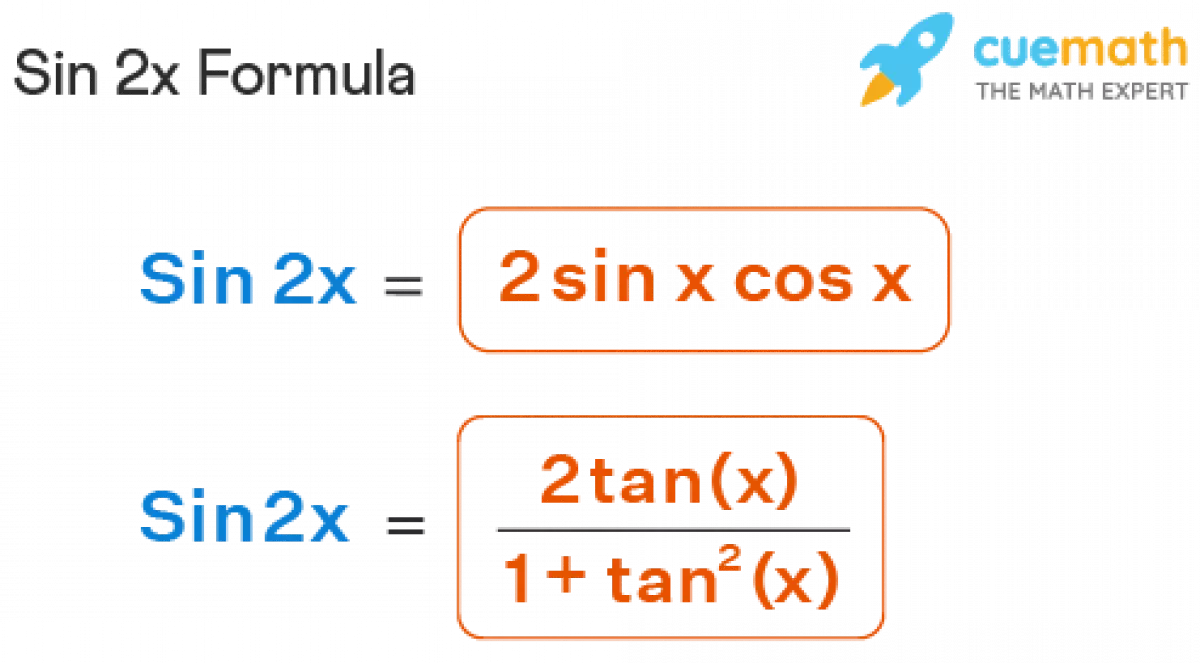Công thức Sin 2x

3. Suy diễn công thức Sin 2x

Để suy diễn công thức Sin 2x, chúng ta có thể sử dụng công thức tổng góc của Sin. Công thức tổng góc của Sin là sin(A + B) = sin A cos B + sin B cos A. Hãy xem suy diễn công thức sin 2x bước từng bước:

Thay A = B = x vào công thức sin(A + B) = sin A cos B + sin B cos A, sin(x + x) = sin x cos x + sin x cos x, ⇒ sin 2x = 2 sin x cos x.

Vậy, chúng ta đã suy diễn công thức của sin 2x.

Chúng ta có thể viết công thức sin 2x chỉ dưới dạng hàm tan hoặc hàm tangent. Để làm điều này, hãy bắt đầu với công thức sin 2x.

sin 2x = 2 sin x cos x, Nhân và chia phương trình trên cho cos x, ta có sin 2x = (2 sin x cos^2x)/(cos x), = 2 (sin x/cosx ) × (cos^2x), Chúng ta biết rằng sin x/cos x = tan x và cos x = 1/(sec x). Vậy sin 2x = 2 tan x × (1/sec^2x), Sử dụng một trong các công thức đồng nhất lượng giác Pythagorean, sec^2x = 1 + tan^2x. Thay thế, ta có sin 2x = (2tan x)/(1 + tan^2x).

Vậy, công thức sin 2x chỉ dưới dạng hàm tan là sin 2x = (2tan x)/(1 + tan^2x).

4. Sin^2x (Sin Bình phương x)

Trong phần này của bài viết, chúng ta sẽ thảo luận về khái niệm sin bình phương x. Chúng ta có hai công thức cho sin^2x có thể được suy diễn bằng cách sử dụng các công thức đồng nhất lượng giác Pythagorean và các công thức góc kép của hàm cosine. Các công thức sin^2x được sử dụng để giải quyết các bài toán tích phân phức tạp và chứng minh các bằng chứng lượng giác khác nhau. Trong phần tiếp theo, chúng ta sẽ suy diễn và khám phá các công thức của sin bình phương x.

Để suy diễn công thức sin^2x, chúng ta sẽ sử dụng các công thức đồng nhất lượng giác sin^2x + cos^2x = 1 và công thức góc kép của hàm cosine được cho bởi cos 2x = 1 - 2sin^2x. Sử dụng các công thức này, chúng ta có thể biểu diễn các công thức của sin^2x dựa trên cos x và cos 2x.

• Công thức sin^2x = 1 - cos^2x
• Công thức sin^2x = (1 - cos 2x)/2

Hãy suy diễn các công thức bước từng bước dưới đây:

Công thức Sin^2x dưới dạng Cosx

Chúng ta có công thức lượng giác Pythagorean được cho bởi sin^2x + cos^2x = 1. Sử dụng công thức này và trừ đi cos^2x từ cả hai phía của công thức đồng nhất lượng giác này, ta có thể viết nó như sau: sin^2x + cos^2x -cos^2x = 1 - cos^2x. Điều này ngụ ý sin^2x = 1 - cos^2x. Công thức này của sin^2x được sử dụng để đơn giản hóa biểu thức lượng giác.

Công thức Sin^2x dưới dạng Cos2x

Bây giờ, chúng ta có công thức lượng giác khác nhau là công thức góc kép của hàm cosine cho bởi cos 2x = 1 - 2sin^2x. Sử dụng công thức này và hoán đổi các thuật ngữ, chúng ta có thể viết nó như sau: 2 sin^2x = 1 - cos 2x ⇒ sin^2x = (1 - cos 2x)/2. Vậy công thức của sin bình phương x sử dụng công thức cos2x là sin^2x = (1 - cos 2x)/2. Công thức này được sử dụng để giải quyết các bài toán tích phân phức tạp.

Những lưu ý quan trọng về Sin 2x:

• Công thức Sin 2x còn được gọi là công thức góc kép của hàm sin.
• Các công thức quan trọng của Sin 2x là sin 2x = 2 sin x cos x và sin 2x = (2tan x)/(1 + tan^2x).
• Công thức cho Sin^2x là sin^2x = 1 - cos^2x và sin^2x = (1 - cos 2x)/2.

☛ Bài viết liên quan:

• Đạo hàm của Sin 2x
• Tích phân của Sin 2x và Sin^2x
• Đạo hàm của Cos2x