Ở bài viết này, chúng ta sẽ tìm hiểu về cách tính tổng bình phương của n số tự nhiên và công thức để tính nó. Tổng bình phương được sử dụng trong thống kê để tìm ra sự biến thiên trong dữ liệu. Chúng ta sẽ cùng nhau khám phá các công thức để tính tổng bình phương của số tự nhiên, cả cho số chẵn và số lẻ, cũng như ứng dụng của tổng bình phương trong hình học. Hãy cùng xem qua vài ví dụ để hiểu rõ hơn về khái niệm này.
Tổng bình phương của n số tự nhiên là gì?
Trước tiên, chúng ta cần nhớ ý nghĩa của số tự nhiên. Số tự nhiên là các số đếm từ 1 đến vô cùng. Nếu chúng ta xét n số tự nhiên liên tiếp, thì việc tìm tổng bình phương của những số này được biểu thị bằng Σi = 1 n i^2. Chúng ta có thể tìm tổng bình phương của n số tự nhiên đầu tiên bằng công thức SUM = 1^2 + 2^2 + 3^2 + ... + n^2 = [n(n+1)(2n+1)] / 6. Chúng ta có thể chứng minh công thức này bằng nguyên lý quy nạp toán học.
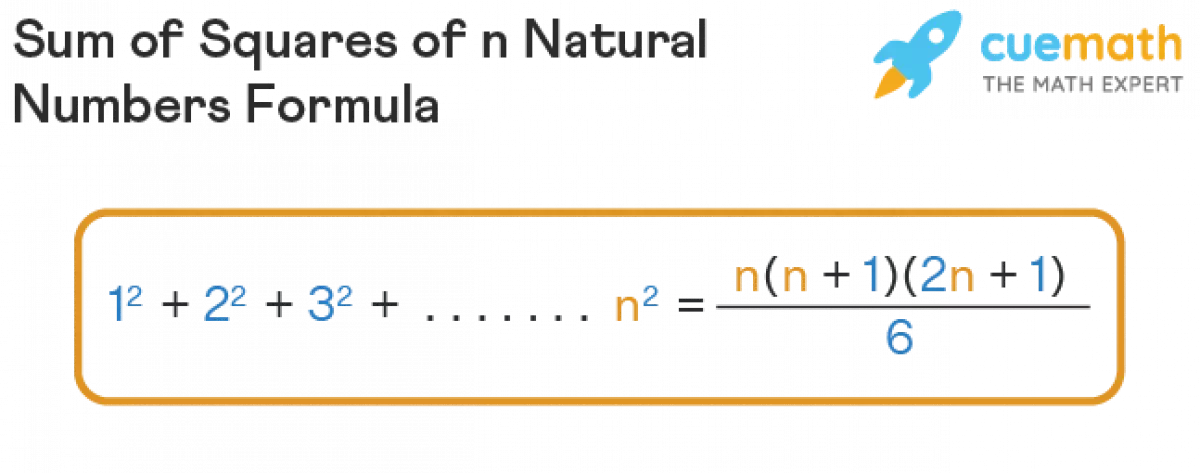Hình ảnh minh họa về công thức tính tổng bình phương của n số tự nhiên.
Công thức tính tổng bình phương của n số tự nhiên
Công thức tính tổng bình phương của n số tự nhiên, cũng như tổng bình phương của n số chẵn và tổng bình phương của n số lẻ được thể hiện như sau:
- Tổng bình phương của n số tự nhiên đầu tiên: [n(n+1)(2n+1)] / 6
- Tổng bình phương của n số chẵn đầu tiên: [2n(n + 1)(2n + 1)] / 3
- Tổng bình phương của n số lẻ đầu tiên: [n(2n+1)(2n-1)] / 3
Đối với các số nhỏ, chúng ta có thể tính trực tiếp bình phương của từng số và cộng chúng lại. Tuy nhiên, với các số lớn hơn, chúng ta cần biết công thức để giúp tính toán dễ dàng hơn. Hãy xem xét ví dụ về công thức này:
Cho a và b là 2 số. Bình phương của chúng là a^2 và b^2. Tổng bình phương của chúng là a^2 + b^2. Chúng ta có thể dễ dàng tìm công thức này bằng cách sử dụng công thức đại số đã biết (a+b)^2 = a^2 + b^2 + 2ab. Từ đó, chúng ta có thể suy ra công thức a^2 + b^2 = (a + b)^2 - 2ab.
Cho a, b, c là 3 số mà chúng ta muốn tính tổng bình phương. Tổng bình phương của chúng là a^2 + b^2 + c^2. Sử dụng công thức đại số đã biết (a + b + c)^2 = a^2 + b^2 + c^2 + 2ab + 2bc + 2ca, chúng ta có thể tính được a^2 + b^2 + c^2 = (a + b + c)^2 - 2ab -2bc -2ca.
Để tính tổng bình phương cho các tổng lớn hơn, chúng ta có thể sử dụng công thức có sẵn, tuy nhiên, việc tìm hiểu cách suy luận công thức cho tổng bình phương của n số tự nhiên: Σn^2 = [n(n+1)(2n+1)] / 6 là rất dễ dàng. Áp dụng công thức này khi giá trị của n đã biết là dễ dàng. Hãy chứng minh công thức này bằng nguyên lý quy nạp toán học.
Để tính tổng bình phương cho các tổng lớn hơn, chúng ta có thể sử dụng công thức có sẵn. Tuy nhiên, việc tìm hiểu cách suy luận công thức cho tổng bình phương của n số tự nhiên: Σn^2 = [n(n+1)(2n+1)] / 6 là rất quan trọng. Dễ dàng áp dụng công thức này khi giá trị của n đã biết. Chúng ta đã chứng minh công thức này bằng nguyên lý quy nạp toán học.
Chứng minh thay thế:
Công thức trên cũng có thể được chứng minh qua phương pháp khác. Hãy xem qua chứng minh thay thế sau:
n^3 - (n-1)^3 = (n- n+1)(n^2 +n(n-1)+ (n-1)^2) n^3 - (n-1)^3 = 1(n^2 +n^2-n+ n^2 + 1 - 2n) = 3n^2 - 3n + 1 n^3 - (n-1)^3 = 3n^2- 3n + 1 -> (1) (n-1)^3 - (n-2)^3 = 3 (n-1)^2 - 3(n-1) +1-> (2) (n-2)^3 - (n-3)^3 = 3 (n-2)^2 - 3(n-2) +1-> (3) ................... 2^3 - 1^3 = 3 (2)^2 - 3(2) +1 1^3 - 0^3 = 3 (1)^2 - 3(1) +1->(cuối cùng) (1) + (2) + (3) +............+ (bước cuối) ⇒ Bằng cách cộng tất cả các bước trên, chúng ta có, n^3 - 0^3 = 3 Σ n^2 - 3Σ n + n n^3 = 3 Σ n^2 - [3n(n+1)/2]+ n [vì Σ n = n(n+1)/2 (tổng của n số tự nhiên)] 3 Σ n^2 = n^3 + [3n(n+1)/2] - n 3 Σ n^2 = n[n^2 + 3(n+1)/2 - 1] - (Lấy n làm chung từ phía bên phải) Σ n^2 = (n/3)( n^2 + (3n+3)/2 -1) = (n/6) (2n^2+ 3n + 1) Tách biệt thành phương trình bậc 2, Σ n^2 = 1^2 + 2^2 + 3^2 + ... + n^2 = [n(n+1)(2n+1)] / 6
