Giới thiệu
Thuật toán Dijkstra được sử dụng để tìm đường đi ngắn nhất từ một đỉnh s đến các đỉnh còn lại trong đồ thị có hướng với trọng số không âm. Trong bài viết này, chúng ta sẽ cùng tìm hiểu về lý thuyết và một số bài tập liên quan đến thuật toán Dijkstra.
Thuật toán Dijkstra (dijkstra algorithm)
Thuật toán Dijkstra hoạt động dựa trên việc gán một nhãn tạm thời cho mỗi đỉnh. Nhãn của mỗi đỉnh giúp cho chúng ta biết được độ dài đường đi ngắn nhất từ đỉnh s đến đỉnh đó. Các nhãn này sẽ được điều chỉnh (cập nhật) thông qua quá trình lặp, trong đó ở mỗi bước lặp, một số đỉnh sẽ có nhãn không thay đổi, và nhãn đó chính là độ dài đường đi ngắn nhất từ đỉnh s đến đỉnh đó.
Bài tập thuật toán Dijkstra
Chúng ta sẽ thực hiện bài tập tìm đường đi ngắn nhất từ đỉnh x1 đến các đỉnh còn lại trong đồ thị vô hướng.
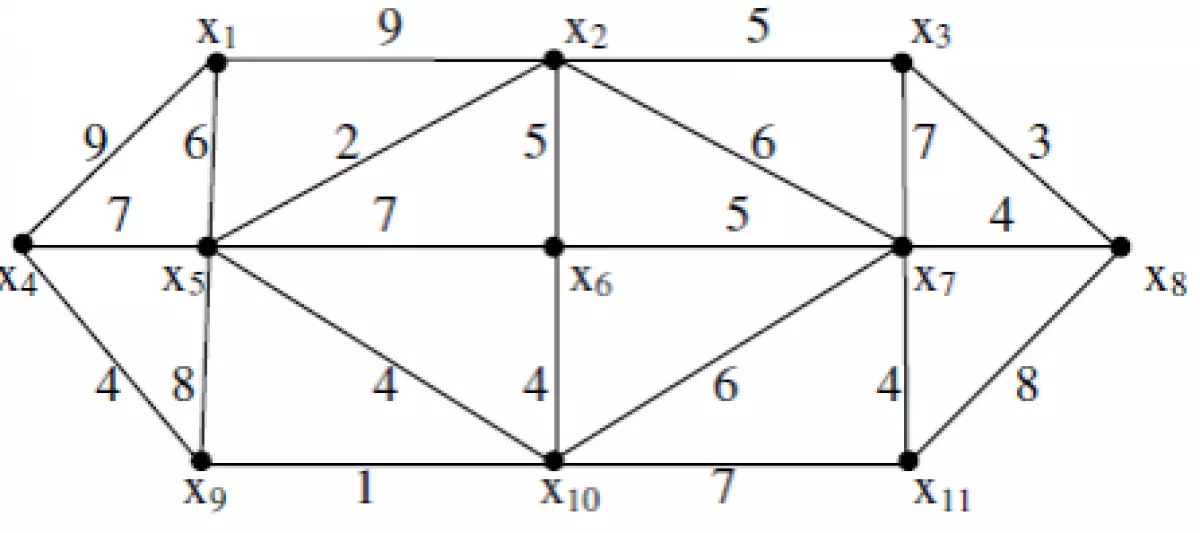
Lời giải:
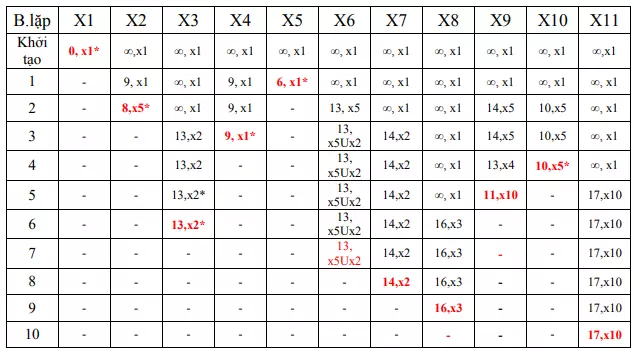
Từ bảng trên, ta có các đường đi ngắn nhất từ x1 đến các đỉnh là: X1X5X2 (độ dài 8); X1X4 (9); X1X5X2X3 (13); X1X5 (6); X1X5X6 (13); X1X5X2X7 (14); X1X5X2X3X8 (16); X1X5X10X9 (11); X1X5X10 (10); X1X5X10X11 (17)
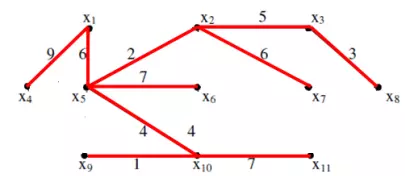
Các đường đi được minh họa trên đồ thị như sau:
Tiếp theo, chúng ta sẽ tìm đường đi ngắn nhất từ đỉnh A đến các đỉnh còn lại trong đồ thị có hướng.
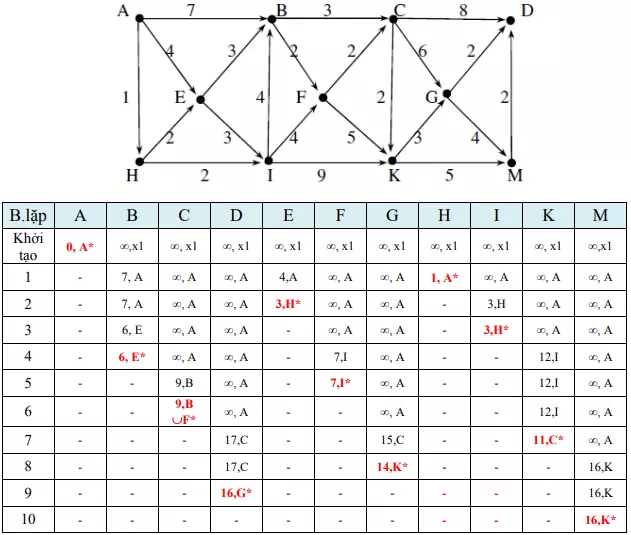
Từ bảng trên, ta có các đường đi ngắn nhất từ A đến các đỉnh là: AHEB (6); AHIFC (9); AHIFKGD (16); AHE (3) AFHIF (7); AHIFCKG (14); AH (1); AHI (3); AHIFCK (11); AHIFCKM (16).
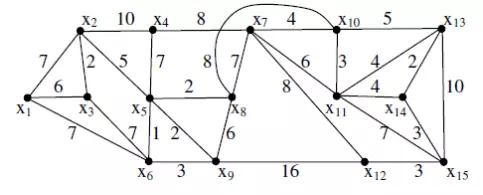
Tiếp theo, chúng ta sẽ tìm đường đi ngắn nhất từ x1 đến x14.
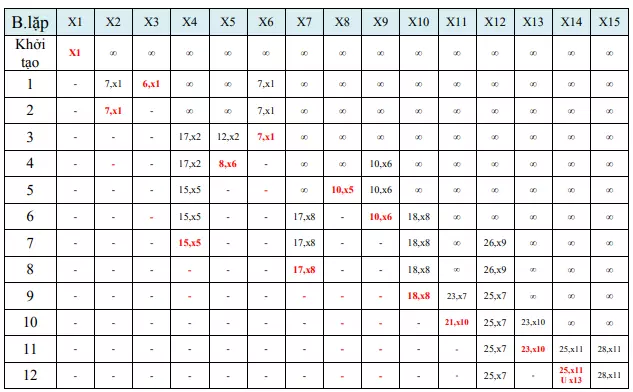
Từ bảng trên, ta có đường đi ngắn nhất từ x1 đến x14 là: X1X6X5X8X10X13X14 hoặc X1X6X5X8X10X11X14 với độ dài là 25.
Tiếp theo, chúng ta sẽ tìm đường đi ngắn nhất từ x1 đến x14 mà chứa đỉnh X8X9.
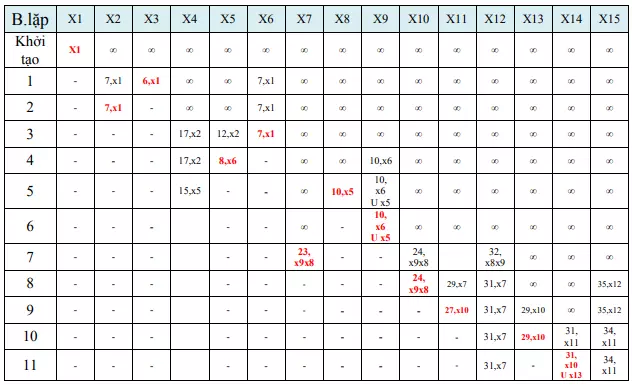
Từ bảng trên, ta có đường đi ngắn nhất từ x1 đến x14 mà chứa đỉnh X8X9 là: x1x6x5x9x8x10x11x14 , hoặc x1x6x5x9x8x10x13x14 , hoặc x1x6x9x8x10x11x14 , hoặc x1x6x9x8x10x13x14 với chiều dài là 31.
Tiếp theo, chúng ta sẽ tìm đường đi ngắn nhất từ x1 đến x14 mà chứa đỉnh X7.
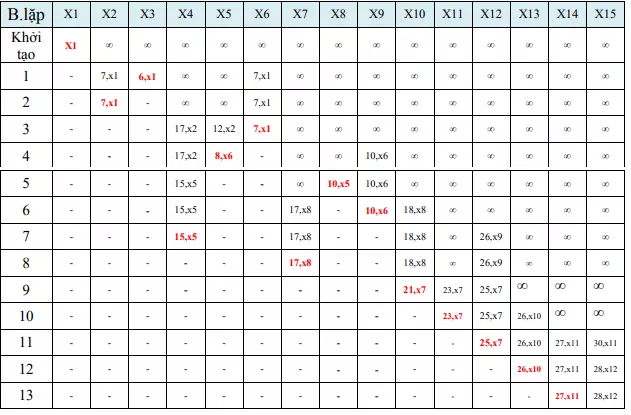
Vậy đường đi ngắn nhất từ x1 đến x14 mà chứa đỉnh X7 là: X1 X6 X5 X8 X7 X11 X14, và độ dài đường đi là 27.
Giải thuật Dijkstra
1. Mô tả giải thuật
Các bước chính của thuật toán Dijkstra để tìm đường đi ngắn nhất từ đỉnh a đến đỉnh z trên đồ thị G=(V,E,W) được mô tả như sau:
Bước 1: Khởi tạo T=V, đặt d[a] = 0, d[u] = ∞ với u ≠ a.
Bước 2: Lặp cho đến khi z không thuộc T:
- Lấy ra đỉnh u thuộc T sao cho d[u] nhỏ nhất.
- Cập nhật lại nhãn d[v] của tất cả các đỉnh v kề với u theo công thức: d[v] = min{d[v], d[u]+w[u,v]}
Mã nguồn giải thuật Dijkstra trên ngôn ngữ lập trình C++:
void Dijkstra(void)
{
/*Đầu vào G=(V, E) với n đỉnh có ma trận trọng số A[u,v]≥ 0; s∈V */
/*Đầu ra là khoảng cách nhỏ nhất từ s đến các đỉnh còn lại d[v]: v∈V*/
/*Truoc[v] ghi lại đỉnh trước v trong đường đi ngắn nhất từ s đến v*/
/* Bước 1: Khởi tạo nhãn tạm thời cho các đỉnh*/
for (v∈ V)
{
d[v] = A[s, v];
truoc[v] = s;
}
d[s] = 0;
T = V { s }; /*T là tập đỉnh có nhãn tạm thời*/
/* Bước lặp */
while (T != φ)
{
// Tìm đỉnh u∈ T sao cho d[u] = min { d[z] | z∈ T };
T = T { u }; /*cố định nhãn đỉnh u*/
for(v∈ T)
{
/* Gán lại nhãn cho các đỉnh trong T*/
if(d[v] > d[u] + A[u, v])
{
d[v] = d[u] + A[u, v];
truoc[v] = u;
}
}
}
}2. Mã nguồn giải thuật Dijkstra
#include
#include
#include
#include
#include
#define MAX 50
#define TRUE 1
#define FALSE 0
int n, s, t;
char chon;
int truoc[MAX], d[MAX], CP[MAX][MAX];
int final[MAX];
void Init(void)
{
FILE *fp;
int i, j;
fp = fopen("ijk1.in", "r");
fscanf(fp, "%d", &n);
printf("Số đỉnh: %d\n", n);
printf("Ma trận khoảng cách:\n");
for (i = 1; i <= n; i++)
{
printf("\n");
for (j = 1; j <= n; j++)
{
fscanf(fp, "%d", &CP[i][j]);
printf("%3d ", CP[i][j]);
if (CP[i][j] == 0)
{
CP[i][j] = 32000;
}
}
}
fclose(fp);
}
void Result(void)
{
int i, j;
printf("\nĐường đi ngắn nhất từ %d đến %d là\n", s, t);
printf("%d ", t);
i = truoc[t];
while (i != s)
{
printf("<= %d ", i);
i = truoc[i];
}
printf("<= %d\n", s);
printf("Độ dài đường đi là: %d\n", d[t]);
getch();
}
void Dijkstra(void)
{
int v, u, minp;
printf("\nTìm đường đi từ s = ");
scanf("%d", &s);
printf("đến ");
scanf("%d", &t);
for (v = 1; v <= n; v++)
{
d[v] = CP[s][v];
truoc[v] = s;
final[v] = FALSE;
}
truoc[s] = 0;
d[s] = 0;
final[s] = TRUE;
while (!final[t])
{
minp = 2000;
for (v = 1; v <= n; v++)
{
if ((!final[v]) && (minp > d[v]))
{
u = v;
minp = d[v];
}
}
final[u] = TRUE; // u là đỉnh có nhãn tạm thời nhỏ nhất
if (!final[t])
{
for (v = 1; v <= n; v++)
{
if ((!final[v]) && (d[u] + CP[u][v] < d[v]))
{
d[v] = d[u] + CP[u][v];
truoc[v] = u;
}
}
}
}
}
void main(void)
{
clrscr();
Init();
Dijkstra();
Result();
getch();
} Trên đây là bài tập và giải thuật Dijkstra trong toán rời rạc, cùng với cách đặt thuật toán trên ngôn ngữ lập trình C++. Hy vọng rằng bài viết này đã giúp bạn hiểu thêm về thuật toán Dijkstra và cách áp dụng nó vào các bài tập. Cảm ơn đã theo dõi!












