Trong thế giới của thuật toán, "Phân chia để trị" (Divide and Conquer) là một cơ chế phổ biến để giải quyết các bài toán. Bài viết này sẽ giúp bạn hiểu rõ hơn về cách tiếp cận này và tại sao nó mang lại hiệu quả cao trong việc giải quyết các bài toán phức tạp.
1. Giới thiệu
Trong cách tiếp cận "Phân chia và chinh phục", chúng ta chia bài toán lớn thành các bài toán nhỏ hơn. Mỗi bài toán con được giải quyết độc lập và khi chúng ta tiếp tục chia nhỏ các bài toán con này, cuối cùng chúng ta sẽ có những bài toán nhỏ nhất mà không thể chia nhỏ được nữa. Những bài toán nhỏ nhất này được giải quyết độc lập và lời giải của chúng được kết hợp để tạo ra lời giải của bài toán ban đầu.
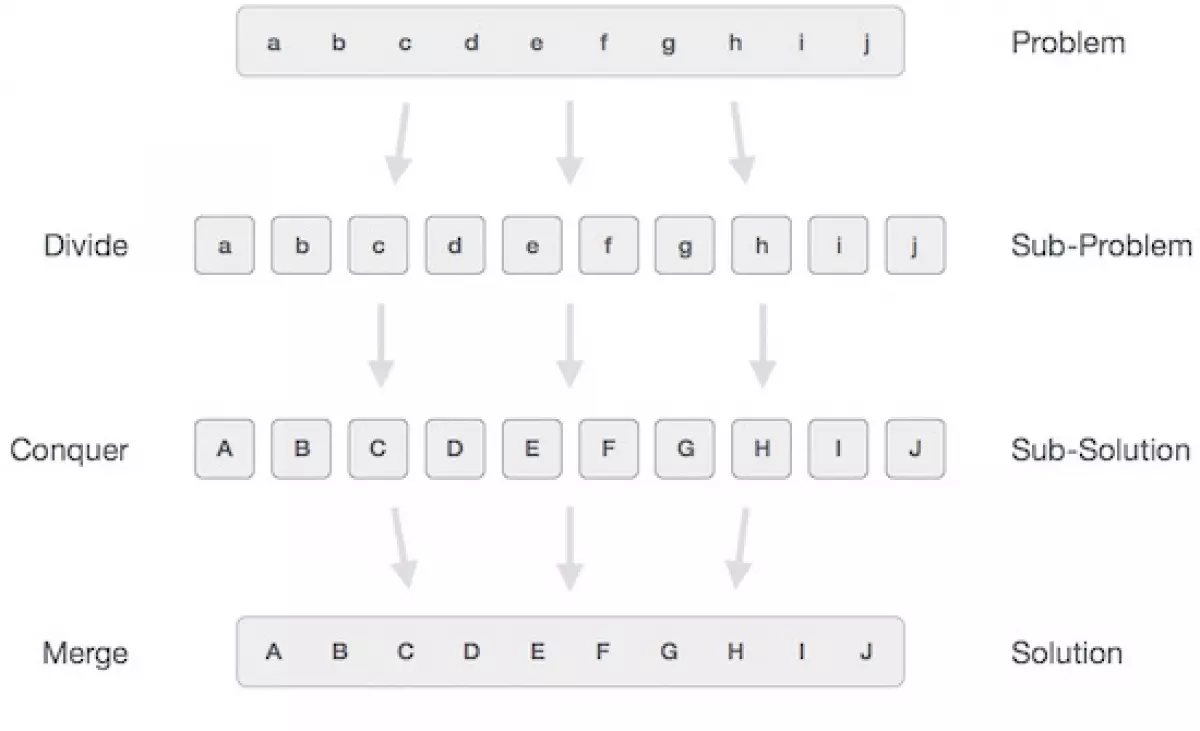Hình ảnh minh hoạ cơ chế phân chia để trị
Chúng ta có thể hiểu cách tiếp cận phân chia để trị qua ba bước sau:
2. Phân chia hoặc ngắt (Divide/Break)
Bước này liên quan đến việc chia nhỏ bài toán ban đầu thành các bài toán con nhỏ hơn. Các bài toán con này đại diện cho một phần của bài toán ban đầu. Bước này thường sử dụng đệ quy để chia bài toán cho đến khi không thể chia nhỏ được nữa. Ở giai đoạn này, các bài toán con trở thành những bài toán nhỏ nhất nhưng vẫn mang trong mình một phần của bài toán ban đầu.
3. Chinh phục / Giải quyết (Conquer/Solve)
Bước này là giai đoạn giải quyết các bài toán con nhỏ hơn. Các bài toán này được coi là "tự giải quyết" ở cấp độ này.
4. Hợp nhất / Kết hợp (Merge/Combine)
Khi các bài toán con nhỏ hơn đã được giải quyết, giai đoạn này kết hợp chúng lại để tạo ra lời giải cuối cùng cho bài toán ban đầu. Cách tiếp cận này hoạt động qua việc kết hợp các bước "chinh phục" và "hợp nhất" gần nhau đến mức chúng trở thành một.
Ví dụ về các thuật toán máy tính dựa trên cách tiếp cận phân chia để trị bao gồm Hợp nhất Sắp xếp (Merge Sort), Sắp xếp nhanh chóng (Quick Sort), Tìm kiếm nhị phân (Binary Search), Phép nhân ma trận của Strassen (Strassen's Matrix Multiplication), Cặp gần nhất (điểm) (Closest pair (points)). Dưới đây là một số nguồn tham khảo tiếng Anh nếu bạn muốn tìm hiểu thêm:
- w3schools
- Geeksforgeeks
- codechef
- dev.to
*Chúng ta đã tìm hiểu về cơ chế "Phân chia để trị" và xem qua một số ví dụ về thuật toán áp dụng cách tiếp cận này. Có rất nhiều cách khác nhau để giải quyết các vấn đề máy tính, nhưng "Phân chia để trị" là một phương pháp mạnh mẽ và tiết kiệm thời gian. Nếu bạn đang tìm kiếm một cách hiệu quả để giải quyết các bài toán phức tạp, hãy thử áp dụng cơ chế "Phân chia để trị" trong thuật toán của bạn!
