Giá trị lớn nhất và nhỏ nhất của hàm số
Giá trị lớn nhất và nhỏ nhất của hàm số trên một đoạn chính là giá trị đó phải đạt được tại ít nhất một điểm trên đoạn đó. Tuy nhiên, cũng có những hàm số không có giá trị lớn nhất hoặc nhỏ nhất dù có cận trên hay cận dưới trên đoạn đó.
Đối với hàm số y = f(x) và x thuộc tập D:
-
Nếu f(x) ≤ M, với x thuộc D và tồn tại ít nhất một x0 thuộc D sao cho f(x0) = M, thì M được gọi là giá trị lớn nhất của hàm số y = f(x) trên tập D.
-
Kí hiệu: Max f(x) = M
-
Nếu f(x) ≥ M, với mọi x thuộc D và tồn tại ít nhất một x0 thuộc D sao cho f(x0) = M, thì M được gọi là giá trị nhỏ nhất của hàm số y = f(x) trên tập D.
-
Kí hiệu: Min f(x) = m
Dưới đây là sơ đồ về cách tìm giá trị lớn nhất và nhỏ nhất của hàm số:
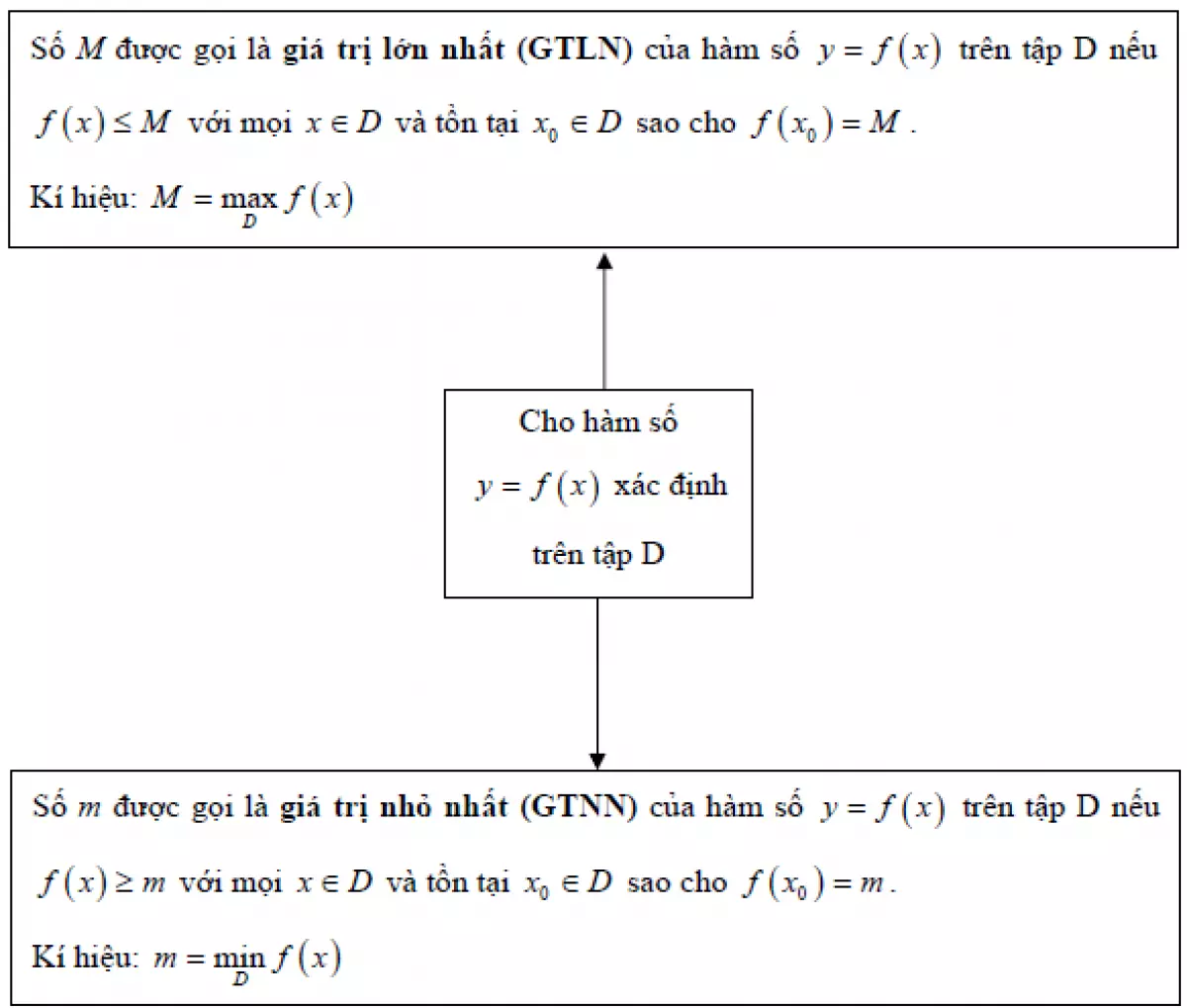
Cách tìm giá trị lớn nhất và nhỏ nhất của hàm số
2.1. Tìm giá trị lớn nhất và nhỏ nhất trên miền D
Để tìm giá trị lớn nhất và nhỏ nhất của hàm số y=f(x) trên tập D, chúng ta sẽ khảo sát sự biến thiên của hàm số trên D, sau đó dựa vào kết quả bảng biến thiên để đưa ra kết luận cho giá trị lớn nhất và nhỏ nhất.
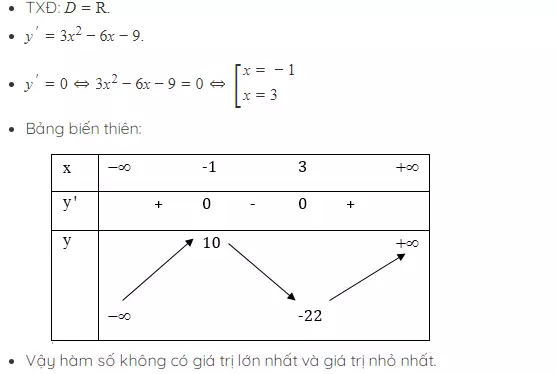
Ví dụ 1: Xem xét hàm số y = x^3 - 3x^2 - 9x + 5
Ví dụ 2: Tìm giá trị nhỏ nhất và lớn nhất của hàm số y = (x^2 + 2x + 3)/(x - 1)

2.2. Tìm giá trị lớn nhất và nhỏ nhất trên một đoạn
Theo định lý, mọi hàm số liên tục trên một đoạn đều có giá trị lớn nhất và nhỏ nhất trên đoạn đó. Vậy quy tắc và phương pháp để tìm giá trị lớn nhất và nhỏ nhất của hàm số f(x) liên tục trên đoạn [a, b] là:
- Tìm các điểm xi thuộc (a, b) sao cho f'(xi) = 0
- Tính f(x), f(b), f(xi) (i = 1, 2,..., n)
- Kết luận: max[f(a), f(b), f(xi)] là giá trị lớn nhất và min[f(a), f(b), f(xi)] là giá trị nhỏ nhất trên đoạn [a, b]
Ví dụ 1: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = -1/3x^3 + x^2 + 2x + 1 trên đoạn [-1, 0]
Ví dụ 2: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = (2x + 1)/(x - 2) trên đoạn [-1/2, 1]
3. Tìm giá trị lớn nhất và nhỏ nhất của hàm số và phương pháp giải
3.1. Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = f(x) trên một khoảng
Để giải bài toán này, ta thực hiện theo các bước sau:
- Tìm tập xác định của hàm số
- Tính đạo hàm y' = f'(x) và tìm các điểm mà đạo hàm bằng 0 hoặc không xác định
- Lập bảng biến thiên của hàm số
- Kết luận giá trị lớn nhất và nhỏ nhất
Ví dụ: Cho hàm số y = (x^2 - x + 1)/(x^2 + x + z). Tìm giá trị của min y [2,3] là bao nhiêu?
3.2. Tìm giá trị nhỏ nhất và lớn nhất của hàm số trên một đoạn
Để tìm giá trị nhỏ nhất và lớn nhất của hàm số trên một đoạn, chúng ta thực hiện các bước sau:
- Tính đạo hàm f'(x)
- Tìm các điểm xi thuộc (a, b) mà tại đó f'(xi) = 0 hoặc f'(xi) không xác định
- Tính f(a), f(xi), f(b)
- Tìm số có giá trị nhỏ nhất m và số có giá trị lớn nhất M trong các số trên
Ví dụ: Tìm giá trị nhỏ nhất và lớn nhất của hàm số y = (x + 2)/(x - 2) trên đoạn [-1/2, 1]
3.3. Tìm giá trị lớn nhất và nhỏ nhất của hàm số lượng giác
Để tìm giá trị lớn nhất và nhỏ nhất của hàm số lượng giác, chúng ta thực hiện các bước sau:
- Tìm điều kiện cho ẩn phụ và đặt ẩn phụ
- Giải bài toán tìm giá trị nhỏ nhất và lớn nhất của hàm số theo ẩn phụ
- Kết luận
Ví dụ: Tìm giá trị lớn nhất và nhỏ nhất của hàm số y = 2cos2x + 2sinx
3.4. Tìm giá trị lớn nhất và nhỏ nhất khi cho đồ thị hoặc biến thiên
Ví dụ 1: Hàm số y = f(x) liên tục trên R và có bảng biến thiên như hình. Giá trị nhỏ nhất của hàm số đã cho trên R là bao nhiêu nếu f(-4) > f(8)?
Ví dụ 2: Cho đồ thị như hình dưới và hàm số y = f(x) liên tục trên đoạn [-1, 3]. Giá trị lớn nhất và nhỏ nhất của hàm số là bao nhiêu?
Hy vọng bài viết trên đã giúp các bạn hiểu thêm về giá trị lớn nhất và nhỏ nhất của hàm số trong môn Toán lớp 12.












