Phương pháp chứng minh bằng phản chứng là một phương pháp chứng minh được sử dụng trong toán học để chứng minh một định lý. Bài viết này sẽ hướng dẫn cách sử dụng phương pháp này thông qua các bước giải cụ thể và các ví dụ minh họa.
Phương pháp chứng minh bằng phản chứng
Để chứng minh một định lý "Đối với mọi x thuộc X, P(x) -> Q(x)" (trong đó P(x) và Q(x) là các mệnh đề chứa biến), ta có thể sử dụng phương pháp chứng minh bằng phản chứng như sau:
Bước 1: Giả sử tồn tại x0 thuộc X sao cho P(x0) đúng và Q(x0) sai.
Bước 2: Dùng suy luận và các kiến thức toán học để đi đến mâu thuẫn.
Ví dụ minh họa
Ví dụ 1: Chứng minh rằng với mọi số tự nhiên n mà n^3 chia hết cho 3 thì n chia hết cho 3.
Giả sử n không chia hết cho 3. Khi đó, n = 3k+1 hoặc n = 3k+2, với k thuộc Z.
- Với n = 3k+1, ta có n^3 = (3k+1)^3 = 27k^3+27k^2+9k+1 không chia hết cho 3 (mâu thuẫn).
- Với n = 3k+2, ta có n^3 = (3k+2)^3 = 27k^3+54k^2+36k+4 không chia hết cho 3 (mâu thuẫn). Vậy n chia hết cho 3.
Ví dụ 2: Chứng minh bằng phương pháp phản chứng: Nếu phương trình bậc hai ax^2+bx+c=0 (a, c ≠ 0) vô nghiệm thì các hệ số a và c cùng dấu.
Giả sử phương trình ax^2+bx+c=0 (a, c ≠ 0) vô nghiệm và các hệ số a, c trái dấu. Với điều kiện a, c trái dấu, ta có ac < 0, suy ra Delta = b^2-4ac = b^2+4(-ac) > 0. Do đó phương trình ax^2+bx+c=0 (a, c ≠ 0) có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm. Vậy phương trình vô nghiệm ax^2+bx+c=0 (a, c ≠ 0) thì a, c phải cùng dấu.
Ví dụ 3: Chứng minh rằng √2 là số vô tỉ.
Dễ dàng chứng minh được nếu n^2 là số chẵn thì n là số chẵn. Giả sử √2 là số hữu tỉ, tức là √2 = m/n, trong đó m, n ∈ N, (m,n) = 1. Từ √2 = m/n ⇒ m^2 = 2n^2 ⇒ m^2 là số chẵn. Suy ra m là số chẵn ⇒ m = 2k, k ∈ N. Từ m^2 = 2n^2 ⇒ 4k^2 = 2n^2 ⇒ n^2 = 2k^2 ⇒ n^2 là số chẵn ⇒ n là số chẵn. Do đó m chẵn, n chẵn, mâu thuẫn với (m,n) = 1. Vậy √2 là số vô tỉ.
Ví dụ 4: Cho a, b, c là các số dương thỏa mãn abc = 1. Chứng minh rằng nếu a + b + c > 1/a + 1/b + 1/c thì có một và chỉ một trong ba số a, b, c lớn hơn 1.
Ta có các trường hợp sau:
- Trường hợp 1: Giả sử ba số a, b, c đều lớn hơn 1 hoặc ba số a, b, c đều nhỏ hơn 1 thì mâu thuẫn với giả thiết abc = 1.
- Trường hợp 2: Giả sử hai trong ba số a, b, c lớn hơn 1. Không mất tính tổng quát, giả sử a > 1, b > 1. Vì abc = 1 nên c < 1, do đó: (a - 1)(b - 1)(c - 1) < 0 ⇒ abc + a + b + c - ab - bc - ca - 1 < 0 ⇒ a + b + c < ab + bc + ca ⇒ a + b + c < 1/a + 1/b + 1/c (mâu thuẫn). Vậy chỉ có một và chỉ một trong ba số a, b, c lớn hơn 1.
Ví dụ 5: Cho các số a, b, c thỏa các điều kiện: a + b + c > 0, ab + bc + ca > 0, abc > 0. Chứng minh rằng cả ba số a, b, c đều dương.
Giả sử ba số a, b, c không đồng thời là số dương, vậy có ít nhất một số không dương. Do a, b, c có vai trò bình đẳng nên không mất tính tổng quát, ta giả sử như a ≤ 0.
- Nếu a = 0 thì mâu thuẫn với abc > 0.
- Nếu a < 0 thì từ abc > 0 ⇒ bc < 0. Ta có ab + bc + ca > 0 ⇒ a(b + c) > - bc ⇒ a(b + c) > 0 ⇒ b + c < 0 ⇒ a + b + c < 0 (mâu thuẫn). Vậy cả ba số a, b, c đều dương.
Ví dụ 6: Chứng minh rằng một tam giác có đường trung tuyến vừa là phân giác xuất phát từ một đỉnh là tam giác cân tại đỉnh đó.
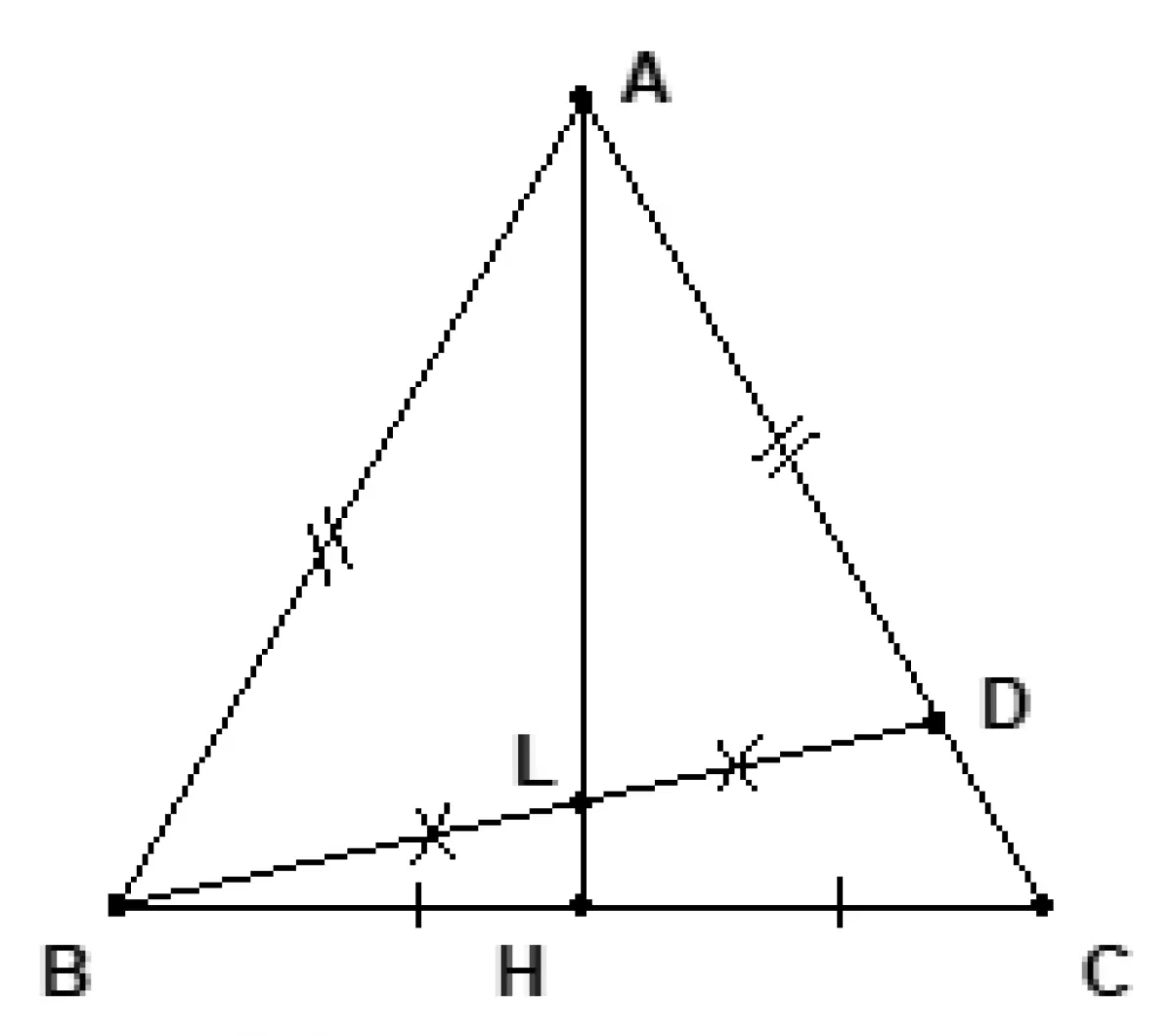
Giả sử tam giác ABC có AH vừa là đường trung tuyến vừa là đường phân giác và không cân tại A. Vì AC ≠ AB, không mất tính tổng quát, ta giả sử như AC > AB. Trên AC lấy D sao cho AB = AD. Gọi L là giao điểm của BD và AH. Khi đó AB = AD, ∠BAL = ∠LAD và AL chung nên ΔABL = ΔADL. Do đó BL = LD hay L là trung điểm của BD. Suy ra LH là đường trung bình của tam giác CBD ⇒ LH//DC. Điều này mâu thuẫn vì LH, DC cắt nhau tại A. Vậy tam giác ABC cân tại A.