Làm thế nào để tìm được khoảng cách từ điểm đến mặt phẳng trong không gian? Đây là một kiến thức khó trong chương trình hình học lớp 11. Nếu bạn không giỏi về chuyên đề này, hãy bổ sung kiến thức và tham khảo các bài tập để rèn luyện kỹ năng cùng Admin nhé!
Khoảng cách từ điểm đến mặt phẳng là gì?
Khoảng cách từ một điểm M đến mặt phẳng (P) trong không gian được định nghĩa là khoảng cách từ điểm M đến hình chiếu vuông góc của M trên mặt phẳng (P). Khoảng cách từ điểm M đến mặt phẳng (P) được ký hiệu là d(M(P)).
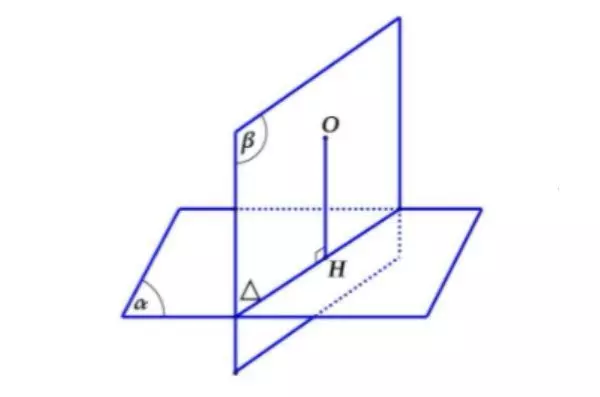
Khoảng cách từ điểm đến mặt phẳng là gì?
Công thức tính khoảng cách từ điểm đến mặt phẳng trong không gian
Trong không gian hệ tọa độ Oxyz, cho một điểm M có tọa độ (α; β; γ) và mặt phẳng (P) có phương trình là ax + by + cz + d = 0. Khi đó, công thức được áp dụng vào việc tính khoảng cách từ 1 điểm đến mặt phẳng tổng quát như sau:
d(M(P)) = |a.α + b.β + c.γ + d|/√(a^2 + b^2 + c^2)
Phương pháp tính khoảng cách từ điểm đến mặt phẳng trong không gian
Dù đã có công thức rất rõ ràng, nhưng muốn tìm được khoảng cách từ 1 điểm đến mặt phẳng trong không gian 3 chiều phải có phương pháp cụ thể. Dưới đây Admin sẽ chỉ cho bạn phương pháp tính khoảng cách từ điểm đến mặt phẳng cực đơn giản như sau:
Cách 1

Hình minh họa cho cách 1
Các bước để tìm khoảng cách từ 1 điểm đến mặt phẳng trong không gian như sau:
- Bước 1: Tìm hình chiếu của O lên mặt phẳng (α) và gọi điểm vuông góc với mặt phẳng (α) là H.
- Bước 2: Tìm một mặt phẳng ((β) có chứa điểm O và vuông góc với mặt phẳng (α)
- Bước 3: Tìm giá trị Δ = (α) ∩ (β)
- Bước 4: Kẻ một đường thẳng OH ⊥ Δ và đi qua điểm H trong mặt phẳng (β). H chính là hình chiếu vuông góc của điểm O lên mặt phẳng (α) như bước 1 đã đề cập.
- Bước 5: Đoạn thẳng OH chính là khoảng cách từ điểm O đến mặt phẳng (α) mà bạn cần tìm.
Cách 2
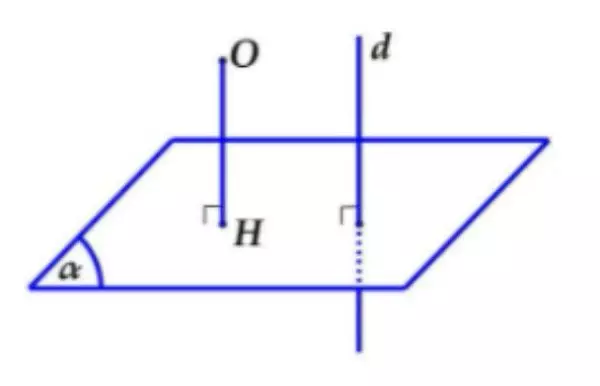
Hình minh họa cho cách 2
Cho trước một đường thẳng d, d vuông góc với mặt phẳng (α), khi đó ta có thể kẻ một tia Ox song song với đường thẳng d và cắt (α) tại điểm H. Lúc này, H chính là hình chiếu vuông góc của điểm O lên mặt phẳng (α). Từ đó có thể tính khoảng cách d(O, (α)) = OH.
Khi tìm khoảng cách từ điểm đến mặt phẳng theo phương pháp này, bạn cũng cần lưu ý một số vấn đề như sau:
Hình minh họa cho lưu ý
- Nếu OA song song với mặt thẳng (α) thì d(O, (α)) = d(A, (α))
- Nếu OA cắt mặt phẳng (α) tại một điểm I thì d(O, (α))/d(A, (α)) = OI/AI (theo định lý talet)
Theo giải này, bạn muốn tìm được khoảng cách từ điểm bất kỳ trong không gian đến một mặt phẳng, bạn sẽ phải đưa bài toán về tìm khoảng cách từ chân đường cao đến mặt phẳng đó. Sau đó sẽ tìm mối quan hệ giữa 2 khoảng cách này với nhau. Thông qua đó bạn có thể tìm ra chính xác khoảng cách từ một điểm được yêu cầu đến mặt phẳng.
Bài tập về khoảng cách từ điểm đến mặt phẳng lớp 11
Lý thuyết về khoảng cách từ điểm đến mặt phẳng trong toán hình lớp 11 khá ít. Để rèn luyện và nâng cao kỹ năng giải bài tập, hãy thử làm một số dạng bài dưới đây, có kèm đáp án để tham khảo:
Bài 1
Cho một lăng trụ đứng ABC.A’B’C’ với đáy ABC là một tam giác vuông cân có cạnh BC = BA = a, độ dài cạnh bên AA’ = a√2. Gọi điểm M là trung điểm của đoạn thẳng BC, hãy tính khoảng cách giữa 2 đường thẳng AM với B’C’.
Giải:

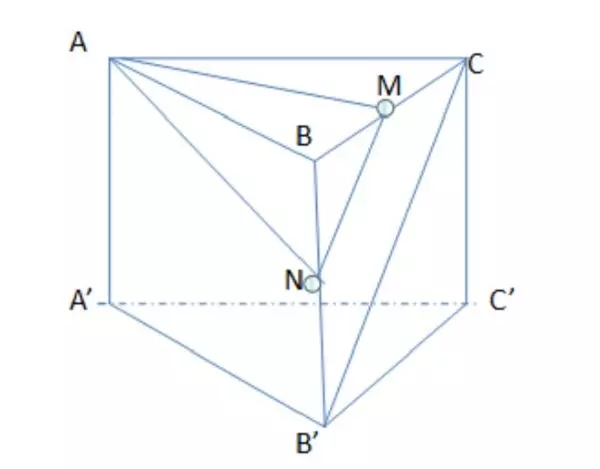
Hình minh họa bài tập 1
Gọi N là trung điểm của cạnh bên BB’, khi đó đoạn thẳng MN chính là đường trung bình của tam giác B’BC.
=> B’C // MN => BC // (AMN)
=> d(B’C; AM) = d(B’C; (AMN)) = d(B’; (AMN))
BB’ ⋂ (AMN) tại điểm N, mà N là trung điểm của BB’ => d(B’; (AMN)) = d(B; (AMN))
Hình chóp A.BMN có BA, BM và BN có một góc vuông
=> 1/d^2(B; (AMN)) = 1/BA^2 + 1/BM^2 + 1/BN^2 = 1/a^2 + 4/a^2 + 2/a^2 = 7/a^2
=> d(B; (AMN)) = a√7/7
Bài 2
Cho một hình chóp S.ABCD có đáy ABCD là một hình chữ nhật, biết cạnh AD = 2a và vuông góc với đáy, cạnh SA = a. Tính khoảng cách từ điểm A đến mặt phẳng (SCD)?
Giải:
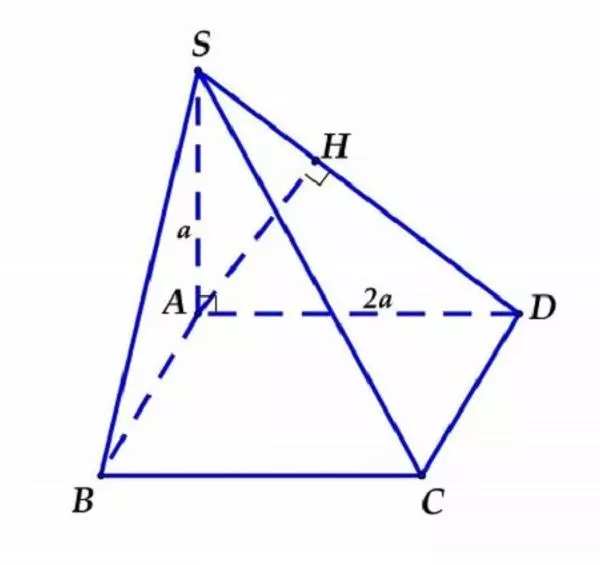
Hình minh họa cho bài 2
Trong mặt phẳng (SAD) kẻ đường thẳng AH vuông góc với SD (H ∊ SD)
Vì CD ⊥ AD và CD ⊥ SA => SA ⊥ (SAD)
=> CD ⊥ AH
Vì AH ⊥ SD và AH ⊥ CD => AH ⊥ (SCD)
=> d(A; (SCD)) = AH = (SA.AD)/√(SA^2 + AD^2) = a.2a/√(a^2 + 4a^2) = 2a/√5
Bài 3
Cho một khối chóp S.ABC, có đáy ABC là một tam giác vuông tại B, biết độ dài các cạnh BA = a, BC = 2a và SA = 2a, đồng thời cạnh SA ⊥ (ABC). Gọi K là hình chiếu của điểm A lên đường thẳng SC. Hãy tính khoảng cách từ điểm K đến mặt phẳng (SAB)?
Giải:

Hình minh họa bài 3
Ta có SA ⊥ (ABC) nên SA ⊥ BC (*)
Ta có tam giác ABC vuông tại B => BC ⊥ AB (**)
Từ (*) và (**) => BC // (SAB)
Trong mặt phẳng (SBC) kẻ một đường thẳng KH song song với cạnh BC (điểm H nằm trên cạnh SB)
=> KH ⊥ (SAB) => d(K; (SAB)) = KH
Ta có: AC = √(AB^2 + BC^2) = √(a^2 + 4a^2) = a√5
Tương tự ta có: SC = √(SA^2 + AC^2) = √(4a^2 + 5a^2) = 3a
Tương tự: SA^2 = SK.SC => SK = SA^2/SC = 4a^2/3a = 4a/3
Vì KH // BC => KH/BC = SK/SC
=> KH = SK.BC/SC = (4/3a.2a)/3a = 8a/9
Bài 4
Cho một hình chóp S.ABCD, có đáy ABCD là một hình vuông với cạnh bằng a. Biết tam giác SAB là tam giác đều và mặt phẳng (SAB) ⊥ (ABCD). Gọi I và F lần lượt là trung điểm của 2 đoạn thẳng AB và AD, hãy tính d(I, (SFC))?
Giải:
Hình minh họa bài 4
Gọi điểm K là điểm giao nhau giữa đoạn thẳng FC và ID
Kẻ IH ⊥ SK (H nằm trên đoạn thẳng SK) (*)
Ta có: (SAB) ⊥ (ABCD) và (SAB) ∩ (ABCD) = AB và SI ⊂ (SAB)
=> SI ⊥ (ABCD) => SI ⊥ FC (1)
Mặt khác, ta xét tam giác vuông AID và DFC có: AI = DF và AD = DC
=> Δ AID = Δ DFC => Góc AID = Góc DFC và Góc ADI = Góc DCF
Mà AID + ADI = 90 độ => DFC + ADI = 90 độ
=> FC ⊥ ID (2)
Từ (1) và (2) ta có: FC ⊥ (SID)
=> IH ⊥ FC (**)
Từ (*) và (**) => IH ⊥ (SFC) hay d(I, (SFC)) = IH
Ta có SI = a√3/2 và ID = a√5/2
1/DK = 1/DC^2 + 1/DF^2 = 5/a^2
=> DK = a√5/5 => IK = ID - DK = 3a√5/10
Do đó: 1/IH^2 = 1/SI^2 + 1/IK^2 = 32/9a^2 => IH = 3a√2/8
=> d(I, (SFC)) = IH = 3a√2/8
Bài 5
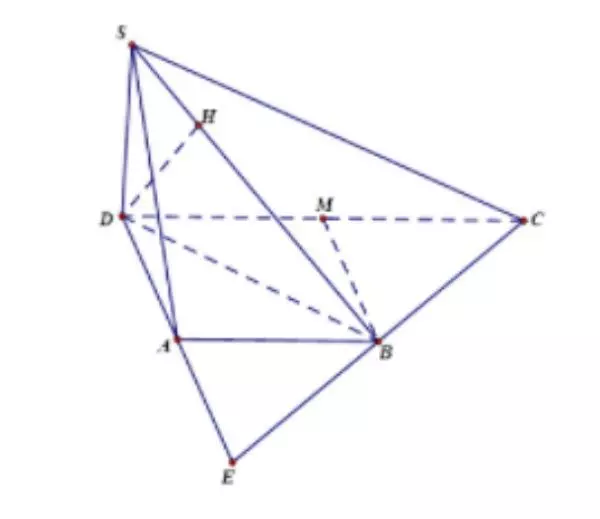
Cho một hình chóp S.ABCD với đáy ABCD là một hình thang vuông tại A và D, biết độ dài cạnh AD = AB = a và độ dài cạnh CD = 2a, SD = a và SD ⊥ (ABCD).
a, Tính d(D,(SBC))
b, Tính Tính d(A,(SBC))
Giải:

Hình minh họa bài 5
a, Gọi điểm M là trung điểm của cạnh CD
Gọi điểm E là giao diện của 2 đường thẳng BC và AD
a, Kẻ DH ⊥ SB trong mặt phẳng (SBD) và điểm H nằm trên cạnh SB (*)
Ví BM = AD = 1/2CD => ∆ BCD vuông tại B => BC ⊥ BD (1)
Mặt khác, vì SD ⊥ (ABCD) => SD ⊥ BC (2)
Từ (1) và (2) => DH ⊥ (SBC) => d(D, (SBC)) = DH
Xét ∆ SBD vuông tại D => 1/DH^2 = 1/SD^2 + 1/BD^2 = 3/2a^2
=> DH = 2a√3/3 => d(D, (SBC)) = DH = 2a√3/3
b, Ta có: d(S, (SBC))/d(D, (SBC)) = AE/DE = AB/CD = ½
=> d(A, (SBC)) = 1/2d(D, (SBC)) = a√3/3
Như vậy toàn bộ thông tin được Admin chia sẻ trong bài đã cung cấp trọn vẹn kiến thức về khoảng cách từ điểm đến mặt phẳng trong không gian. Không chỉ có vậy, Admin còn đề cập đến một số bài tập cơ bản kèm cách giải để bạn tham khảo. Hãy học hỏi và lưu lại kiến thức quan trọng để học hình 11 giỏi hơn mỗi ngày nhé!












